Zeltstangen 4 m
Sechseckiges Zelt
Die Skizze für 1 Stange
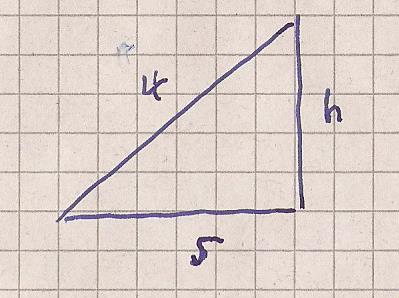
4 ^2 = h^2 + s^2
s ^2 = 16 - h ^2
Fläche = 3/2 * s ^2 * √ 3
Fläche = 3/2 * ( 16 - h ^2 ) * √ 3
Fläche = 3/ 2 * √ 3 * ( 16 - h ^2 )
Volumen = 1/3 * Fläche * h
Volumen = 1/3 * 3/ 2 * √ 3 * ( 16 - h ^2 ) * h
 h ergibt sich zu 2.31 m
h ergibt sich zu 2.31 m
Alle Angaben ohne Gewähr.
Nachsehen und bei Bedarf nachfragen.