Betragsfunktion - Ich finde das Intervall nicht.

Question

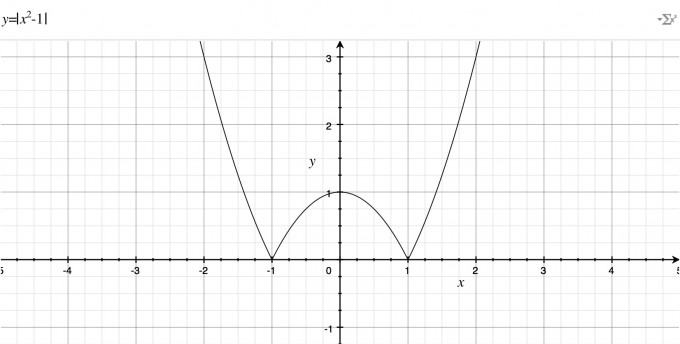
f(x) = |x^{2} - 1|

Ich weiss dass,...

..ich alles was unterhalb der x-Achse liegt, nach oben spiegele. 
..dass das Spiegeln der Punkte unten nach oben, die Umkehrung der Vorzeichen der jeweiligen Y-Werte bedeutet.

Aber bei der Fallunterscheidung bekomme ich jeweils verschiedene Intervalle die sich teilweise überlappen.
Und ich komme gar nicht nach was das bedeutet: 

Was meiner Meinung nach richtig wäre:
Also meiner Meinung nach, ist die Funktion positiv in den Intervallen (-∝,-1] und [1,+∝) 
Und die Funktion ist negativ im Intervall (-1,1) Diese Punkte in diesem Bereich gilt es zu spiegeln. 

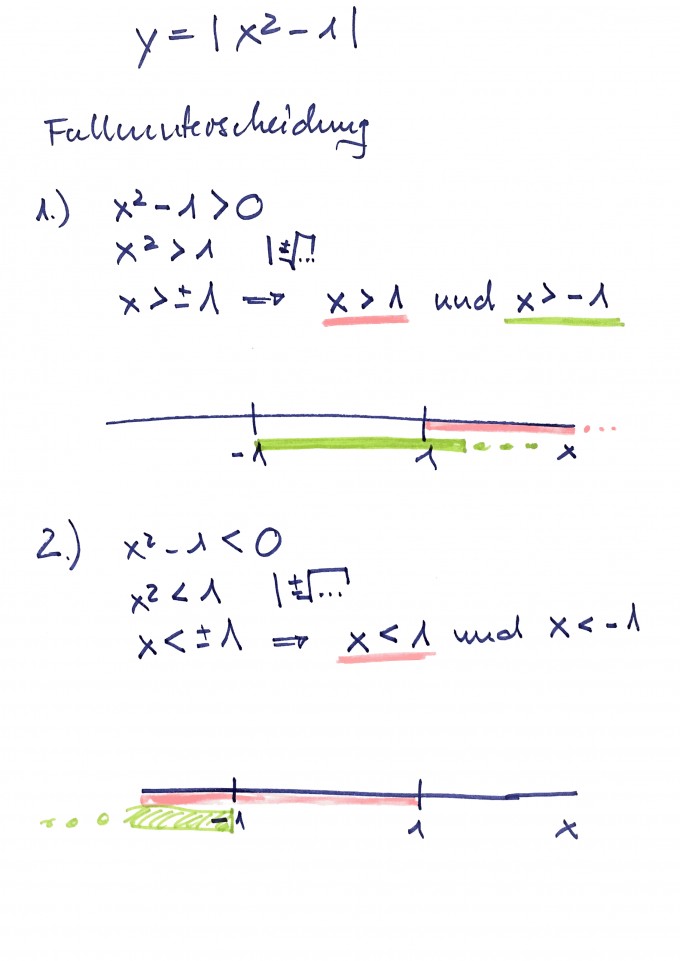
Was ich rechnerisch herausgefunden habe:
Gemäss meiner Rechnung unten im Bild, ist aber dass die Funktion positiv ist im Intervall 

x > 1: (1,∝)
x > -1: (-1,∝).

Und das die Funktion negativ ist im Intervall

x < 1:  (-∝,1]
x < -1: (-∝, -1]. 

Das kann doch nicht stimmen, was mache ich falsch ?

 

Answer 1

x^2 > 1 --> x > 1 oder x < - 1

x^2 < 1 --> - 1 < x < 1

Answer 2

Ausgangsfunktion :
Wenn ich den mittleren Teil " nach unten
klappe " habe ich die Funktion
f ( x ) = x^2 - 1
Das " nach oben klappen " wird
bewerkstelligt durch
f ( x ) = | x^2 - 1 |

Das wars doch schon.

Comments

Ausgangsfunktion
f ( x ) = x^2 - 1
x^2 = 1 | √
√ x^2 = √ 1
| x | = 1

x = 1
und
x = -1

---

x = 1
und
x = -1

Gerade das ist eben falsch.

Answer 3

f(x) = |x^{2} - 1|

f(x) = |(x+1)(x-1)|

Falls beiden Faktoren negativ ODER beide Faktoren positiv, d.h. falls x<-1 ODER x>1 

f(x) = |(x+1)(x-1)|  = (x+1)(x-1)

Falls der kleinere Faktor negativ UND der grössere positiv, d.h. falls -1 < x UND  x<1
f(x) = |(x+1)(x-1)|  = -(x+1)(x-1)