Dass \(1\) eine Nullstelle ist, kann man einfach durch einsetzen von \(x = 1\) in die Funktionsgleichung überprüfen:
[spoiler]
\(f(1) = 1^3 - 2\cdot 1^2 -5\cdot 1 + 6 = 1 - 2 - 5 + 6 = 0\)
[/spoiler]
Zum Berechnen der weiteren Nullstellen kann man einen Linearfaktor \((x - 1)\) ausklammern. Dazu kann man eine Polynomdivision durchführen.
[spoiler]
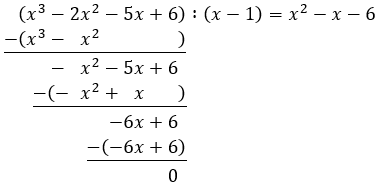
Demnach ist \(f(x) = (x - 1)\cdot(x^2 - x - 6)\).
[/spoiler]
Die weiteren Nullstellen von \(f\) erhält man, indem man die Nullstellen des verbliebenen quadratischen Terms berechnet. (Beispielsweise mit quadratischer Lösungsformel.)
[spoiler]
Die weiteren Nullstellen von \(f\) erhält man als Lösungen der Gleichung \(x^2 - x - 6 = 0\). Dazu kann man beispielsweise eine quadratische Lösungsformel verwenden ... \[\begin{aligned}x^2 - x - 6 = 0 \quad&\Longleftrightarrow\quad x =\frac{-(-1)\pm\sqrt{(-1)^2-4\cdot1\cdot(-6)}}{2\cdot 1}\\&\Longleftrightarrow\quad x=\frac{1\pm \sqrt{25}}{2} =\frac{1\pm 5}{2}\\&\Longleftrightarrow\quad x=\frac{1- 5}{2}=\frac{-4}{2}=-2\quad\text{ oder }\quad x= \frac{1+5}{2}=\frac{6}{2} = 3\end{aligned}\]
Demnach erhält man ingesamt, dass \(x_1 = 1\), \(x_2 = -2\), \(x_3 = 3\) die Nullstellen von \(f\) sind. Demnach ist dann übrigens \(f(x) = (x-1)\cdot(x+2)\cdot(x-3)\).
[/spoiler]
Damit kann man nun den Graphen skizzieren, indem man die Nullstellen einzeichnet, und dann den Verlauf einer ganzrationalen Funktion 3-ten Grades skizziert, welche wegen des positiven Leitkoeffizienten für \(x\to \infty\) gegen \infty divergiert und für \(x \to -\infty\) gegen \(-\infty\) divergiert.
[spoiler]
~plot~ x^3 - 2 * x^2 - 5 * x + 6; {1|0}; {-2|0}; {3|0}; [[-4|5|-6|10]] ~plot~
[/spoiler]