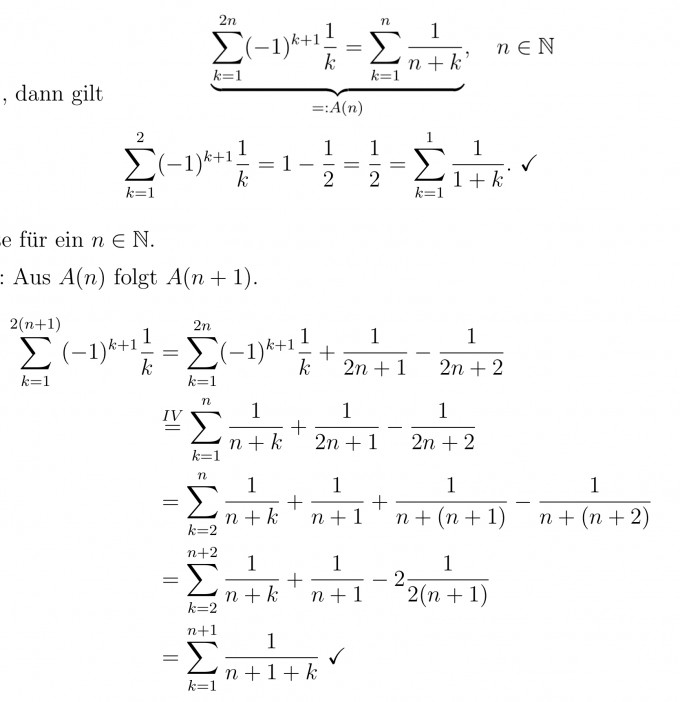
Bei IS verstehe ich gar nicht den Schritt vor dem IV auf das Gleichzeichen steht.
Ich hätte es so gemacht: (-1)^{k+1} * 1/k + (-1)^{2(n+1)+1} * 1/(2(n+1)) und danach das:
1/(n+k) + (-1)^{2(n+1)+1} * 1/(2(n+1))
Wäre echt dankbar wenn mir jemanden erklären warum das flasch wäre und wieso und wie man das machen sollte :)