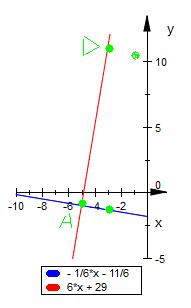
Eine andere Lösungsvariante
A (-5 | -1)
B ( 1 | -2)
Seite a
Abstand = √ [ ( -5-1 ) ^2 + ( -1 - (-2) ) ^2 ]
= √ ( 36 + 1 )
= √ 37 = 6.083
Seite d
a * d = 74
d = 74 /√ 37 = 12.166
Steigung Seite a = Δ y / Δ x
ma = 1 / -6 = -0.16666
Steigung Normale ( Seite d )
md = -1 / ma = 6
Winkel delta = 80.538 °
Bekannt von DC
d = 12.166
delta = 80.538 °
sin ( delta ) = Δ y / 12.166
Δ y = 11.987
cos ( delta ) = Δ x / 12.166
Δ x = 2
Dx = Ax + 2 = -5 + 2 = -3
Dy = Ay + 11.987 = -1 + 11.987 = 10.987
D ( -3 | 10.987 )