f(x)= 1/2x^4-x^3-x^2-4 Nullstellen

Question

Nullstellen ausrechnen mit Rechnung bitte, wie kommt man auf das Ergebnis x1=-1,53, x2=2,98

Answer 1

Hi,

es gibt hierfür zwar eine Formel. Die wird meist aber wegen ihrer Komplexität nicht benutzt. Ein Mittel der Wahl wäre bspw das Newtonverfahren. Das ist zwar nur ein Näherungsverfahren, aber meist ausreichend.

Grüße

Comments

Welche Formel gibt es denn?

LG

---

könntest du dann vielleicht das newoton verfahren auf die aufgabe anwenden ?

---

Da hast du recht. Dachte mich an eine Formel erinnert zu haben. Dabei bezog ich mich wohl auf diesen Artikel: https://de.wikipedia.org/wiki/Polynom_vierten_Grades

Das hatte ich falsch in Erinnerung ;).

---

@Miguur: Siehe das Bsp im Link der Antwort. Da ist das denke ich sauber dargestellt :).

Answer 2

  Wenn ich dich auf die cartesische Vorzeichenregel  (  CV  )  aufmerksam machen dürfte.  Übrigens; im Diplom in der Algebraprüfung  packte ich eine 1 Plus, ohne je von ihr gehört zu haben ...   Geschweige euch Schülern - euch enthält man sie ja auch vor .

   In deinem Fall gibt dir die CV genau eine positive und eine negative Wurzel .

Answer 3

a) Vor über 600 Jahren näherte man sich per Bisektion (Intervallhalbierung)

http://www.gerdlamprecht.de/Roemisch_JAVA.htm Beispiel 2 mit Vorgabebereich -2...-1:

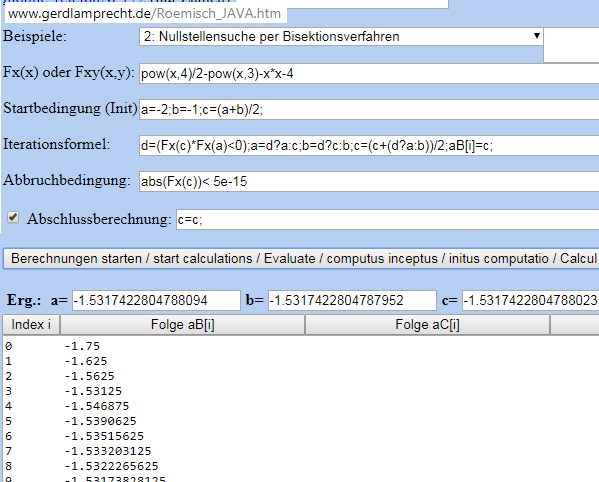
b) vor etwa 400 Jahren konnte man Ableiten und das Newton Verfahren anwenden: Beispiel 118 Start um 3 herum

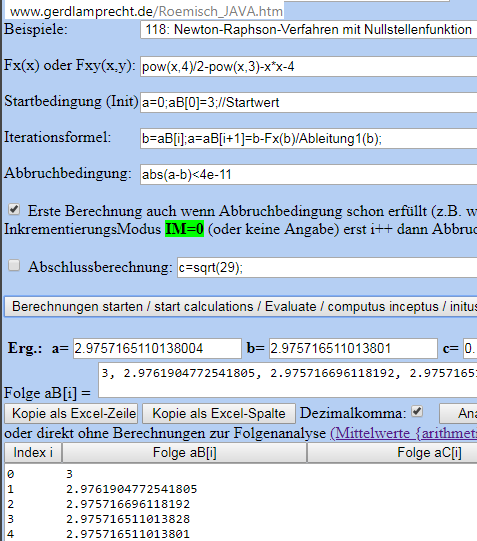
c) Mit den Cardanischen Formeln + kubische Hilfsgleichung + Fallunterscheidung kam man den exakten Lösungen vor etwa 300 Jahren näher.

d) Heute hat man bei c) die Fallunterscheidungen und trigonometrische Funktionen durch exakte 3. Wurzeln und komplexen Zahlen fertige PQRSTUVW Formeln analog den pq-Formeln bei quadratischen Gleichungen:

http://www.lamprechts.de/gerd/php/gleichung-6-grades.php rechnet c) und d) vor:

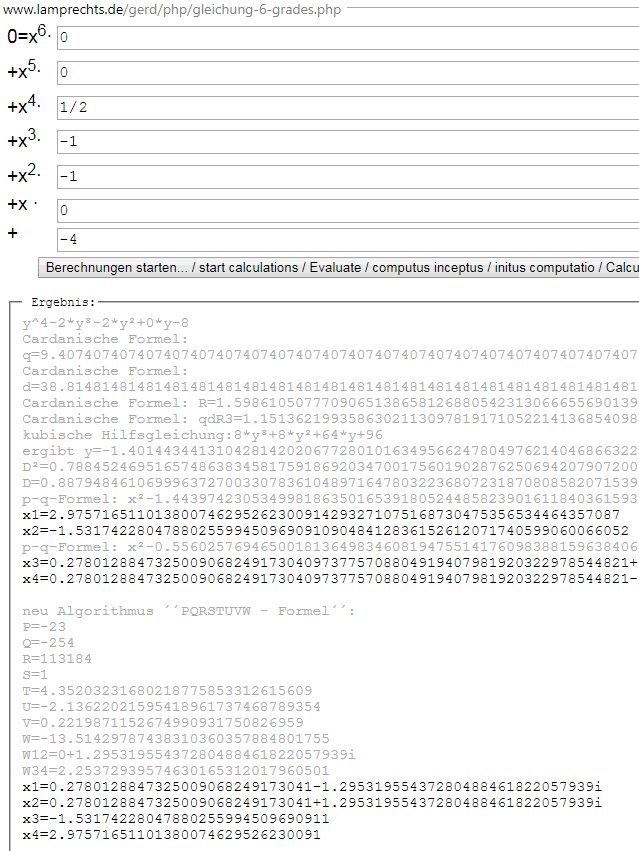
x₃ mal ausgeschrieben (interessiert leider kein Lehrer, da kein Schulstoff):

1/2 + 1/(2 sqrt(3/(7 - 46/(6 sqrt(786) - 127)^{1/3} + 2 (6 sqrt(786) - 127)^{1/3}))) - 1/2 sqrt(14/3 + 46/(3 (6 sqrt(786) - 127)^{1/3}) - 2/3 (6 sqrt(786) - 127)^{1/3} + 6 sqrt(3/(7 - 46/(6 sqrt(786) - 127)^{1/3} + 2 (6 sqrt(786) - 127)^{1/3})))

mit sqrt(x)= "2. Wurzel von x"

x^{1/3}= "x hoch 1/3" = "3. Wurzel von x"

Answer 4

Hallo Miguur,

Newtonverfahren:
Berechnen der Nullstellen von f(x)  (f muss differenzierbar sein)
Ausgehend von einem (möglichst guten) Startwert, den man z.B zwischen zwei x-Werten findet, deren Funktionswerte verschiedenes Vorzeichen haben, findet man - auch mit einem einfachen Taschenrechner -  immer bessere Werte mit der Formel$$x_{neu} =  x_{alt} - \frac{f(x_{alt}}{ f ' (x_{alt})}$$Du weißt allerdings i.A. nicht, ob du alle NS gefunden hast. Hier hilft oft eine Betrachtung der Extremwerte und der Krümmung. Bei Polynomfunktionen kann auch die Vorzeichenregel von Descartes helfen:

https://de.wikipedia.org/wiki/Vorzeichenregel_von_Descartes

Manchmal konvergiert das Verfahren nicht (wenn man für x_alt zum Beispiel eine Nullsstelle von f ' erwischt, was hier für die Werte x=0 und x=2 der Fall ist). Dann hilft oft ein anderer Startwert.
Je besser der Startwert, desto weniger Rechnung.

f(x) = 1/2·x⁴ - x³ - x² - 4   ,   f '(x) = 2·x³ - 3·x² - 2·x

Startwert x_alt = 1  : 

Startwert x_alt = 3 :

Gruß Wolfgang