Funktionenschar: Bestimme die Ortskurve der Minima. Wie geht das ?

Question

Ich habe wieder eine Frage zu Funktionenscharen,
und wenn ich das jetzt hab, kann ich so ziemlich alles in diesem Bereich.

Frage siehe ganz unten (c)

Aufgabe

Gegeben ist die Kurvenschar

fa(x) = 4/3x³ -ax² 

(a) Kurvendiskussion (Nullstellen, Extrema, Wendepunkte).
(b) Zeichnen Sie den Graphen für a = 4.
(c) Bestimmen Sie die Orstkurve der Minima der Schar f_a.
(d) Bestimmen Sie die Gleichung der Wendetangente für f₄.
(e) Bestimmen Sie den Schinttwinkel von f₄ mit der x-Achse.

(a) Kurvendiskussion
N1 ( 0 I 0 )
N2 ( 3/4*a I 0 )

E1( 0 I 0 ) 
E2 ( 1/2*a I -1/2*a³)

W ( 6/24*a I - 1/24*a³)

(b) a=4

N1 ( 0 I 0 )
N2 ( 3 I 0 )

E1 ( 0 I 0 ) 
E2 ( 2 I -16/3 )

W ( 1 I -8/3 ) 

Frage

(c) Wie bestimme ich die Ortskurve der Minima der schaf f_a ?
      Kann mir das jemand erklären ?

Answer 1

So, wenn ich mich nicht irre:

f_{a}(x)=(4/3)x^3-ax^{2}

f'_{a}(x)=2x(2x-a)  → N₁(0|0)  N_{2}(a/2|x)

T_{1}=(a/2 | -a^3/12)

x=a/2     ---> a=2x  (für a in y=-a^3/12 einsetzen)

y=-a^3/12

---------------------------------------------------

y=-(2/3)x^3

Answer 2

Hallo limonade,

f_a(x) = 4/3 x³ - a x² 

Minima:

für a<0      (0|0)     

für a>0    (a/2 | - a³ /12)   (ist wohl bei dir ein Schreibfehler !!)

x_min = a/2   →  a = 2 x_min

 y_min =  - a³/12

  a in y_min einsetzen:

y_min = - 8x_min³ / 12   = -2/3 x_min³

Ortskurve der Minima   y = -2/3 x³

Auf dieser liegen alle Minima

Gruß Wolfgang

Answer 3

fa(x) = 4/3 * x^3 - a * x^2 
f ´( x ) = 4 * x^2 - 2a * x
f ´´ ( x ) = 8 * x - 2a

Stellen mit waagerechter Tangente
4x^2 - 2ax = 0
x * ( 4x - 2a ) = 0
x = 0
und
4x - 2a = 0
x = 1/2 * a

Min oder max
f ´´ ( 0 ) =  - 2a
f ´´ ( 1/2 a ) = 8 * 1/2 * a - 2a
f ´´ ( 1/2 a ) = 4 * a - 2a
f ´´ ( 1/2 a ) = 2a

Ob eine Extremstelle Min oder Max ist
hängt von a ab.
Für a > 0 ist
f ´´ ( 0 ) = Hochpunkt
f ´´ ( 1/2 a ) = Tiefpunkt

Ich rechne einmal für diesen Fall
x = 1/2 * a
y = - a^3 / 12

x = 1/2 * a => a = 2*x
Einsetzen
y = -(2x)^3 / 12
ort ( x ) = -8x^3 / 12
ort ( x ) = - 2/3 * x^3

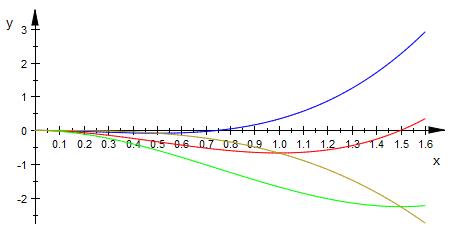
blau, rot, grün sind die Graphen für
a=1, 2, 3
oker ist die Ortskurve welche alle Tiefpunkte
miteinander verbindet.