Stochastik (Baumdiagramme erstellen)

Question

Liebe Leute,

ich habe eine Frage zum erstellen eines Baumdiagrammes aus einer Textaufgabe:

Hier einmal die Aufgabe und Lösung:

Die Rohlinge (das sind Werkstücke, die noch weiterbearbeitet werden müssen) für eine Fräsmaschine
werden in 3 Behältern geliefert. Im ersten befinden sich 6 Rohlinge, im zweiten 5 Rohlinge und im dritten
7 Rohlinge. Aufgrund von Transportschädigung befindet sich in jedem Behälter je 1 defekter Rohling.
a) Jedem Behälter wird genau 1 Rohling entnommen. Von diesen 3 Rohlingen ist keiner defekt.

– Berechnen Sie die Wahrscheinlichkeit für dieses Ereignis.
Die Lösung ist 5/6 * 4/5 * 6/7 = 0.57  bzw. 57 %

Mir ist leider noch nicht ganz klar, warum ich die Ereignisse zusammenzählen soll. Im Prinzip sind das 3 verschiedene Boxen oder Ziehungen wenn man so will. Bei der Ziehung aus einer Box scheint klar, dass alle Ziehungen hintereinander in  einem Baumdiagramm dargestellt werden können. Bei diesen scheinbar unabhängigen Ereignissen bin ich mir immer unsicher, ob Pfadregel (Multiplikation) oder Summenrenregel anzuwenden ist. Nach welchen Kriterien kann ich das entscheiden, also was sind die Regeln wenn Ereignisse zusammengezählt oder multipliziert werden.
Von meiner Logik hätte ich die 3 Boxen mit 3 Baumdiagrammen dargestellt und dann alle 3 Pfade addiert. Welche Tricks oder Merkregel gibt es, um das zu verstehen. Entscheidet einzig und allein die Angabe / Aufgabenstellung mit ihren genauen Wortlaut oder die Situation über die Wahrscheinlichkeitsmultiplikation oder Summierung ?
Bitte um eine Regel, wie ich das machen soll oder mir merken kann, da ich jedes mal raten, was richtig ist. Wie macht ihr das genau? Welchen Prozess muss ich beachten?

Vielen Dank

Liebe Grüße

Rudi

Answer 1

ob Pfadregel (Multiplikation) oder Summenrenregel anzuwenden ist.

Du darfst Wahrscheinlichkeiten von Ereignissen addieren, wenn sich die Ereignisse gegenseitig ausschließen (wenn sie also nicht gleichzeitig eintreten können).

Jedem Behälter wird genau 1 Rohling entnommen.

Die Ereignisse "Rohling aus Behälter 1 ist kaputt" und "Rohling aus Behälter 2 ist kaputt" können gleichzeitig eintreten. Also darfst du ihre Wahrscheinlichkeiten nicht addieren.

die 3 Boxen mit 3 Baumdiagrammen dargestellt

Aufgrund von Transportschädigung befindet sich in jedem Behälter je 1 defekter Rohling. Damit kannst du die Wahrscheinlichkeit, bei zufälligem Ziehen aus dem 7er-Behälter einen defekten zu erwischen direkt berechnen. Dazu braucht man kein Baumdiagramm.

Das Baumdiagramm brauchst du, um daraus den Versuch "Jedem Behälter wird genau 1 Rohling entnommen" zu modellieren. Dieser Versuch setzt sich nähmlich aus den Versuchen "Aus  dem 7er-Behälter wird genau 1 Rohling entnommen", "Aus  dem 6er-Behälter wird genau 1 Rohling entnommen" und "Aus  dem 5er-Behälter wird genau 1 Rohling entnommen" zusammen. Diese drei Versuche sind dann die Ebenen des Baumdiagramms.

Baumdiagramme werden immer dann benötigt, wenn ein größerer Versuch aus mehreren kleineren Versuchen zusammengesetzt ist. Die kleineren Versuche sind dann die Ebenen des Baumdiagramms. Und wenn Baumdiagramme im Spiel sind, dann musst du natürlich die für Behandlung von Baumdiagrammen geltenden Regeln befolgen.

Answer 2

Ich denke, dass es immer hilfreich ist, sich erst mal vorzustellen welches

die möglichen Ergebnisse sind:

Wenn man aus drei Boxen die Teile entnimmt, kann es passieren das die

Ergebnisse etwa so aussehen (d =defekt ; r= richtig)

drd

drr

ddr

rdd

etc.

Wenn man die Ergebnisse in solchen Tupeln schreiben kann, hat man schon die

Struktur des Baumdiagramms:

1.Ziehung   2.Ziehung  3.Ziehung

und bei jeder Ziehung interessiert ja nur   r oder d.

Also ist das ein Baum der erst mal 2 Äste hat  d bzw. r für die 1. Ziehung

dann die 2. etc.   Sähe wohl so aus

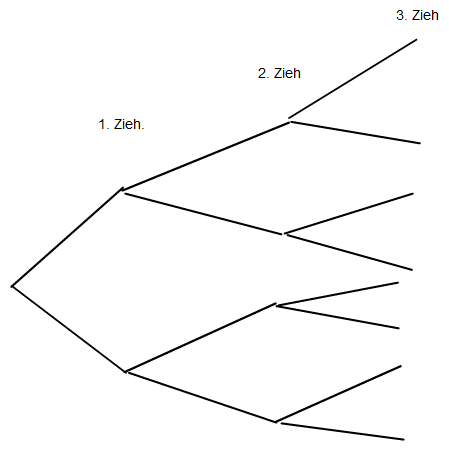
Jetzt noch überlegen welcher dieser Pfade interessiert:

Hier ist es ja nur der mit  rrr

Und die Wahrscheinlichkeiten längs des Pfades muss man

multiplizieren.

Addieren würde man die Werte mehrerer Pfade, wenn etwa

die Frage wäre:  genau einer ist defekt, da müsste man

zuerst die Pfade  drr   rdr   rrd

ausrechnen und diese drei dann addieren.