... leider verstehe ich sie überhaupt nicht ...
Es sollen drei Vektoren bestimmt werden - ich nenne sie mal \(b_1\), \(b_2\) und \(b_3\) - die jeweils in einer der drei Koordinatenebenen liegen und die zusätzlich die Gleichung \(c = a \times b \) erfüllen. Das \(\times\) ist das Zeichen für das Kreuzprodukt. Wie man ein Kreuzprodukt berechnen habe ich hier in dieser Antwort schon mal beschrieben. Eine Koordinatenebene ist eine Ebene im Raum , die durch zwei der drei Koordinatenachsen \(x\), \(y\) und \(z\) aufgespannt wird.

oben auf dem Bild habe ich die drei Koordinatenebenen durch drei Quadrate dargestellt. Rot für die XY-Ebene, grün für die YZ-Ebene und blau für die ZX-Ebene. Klicke auf das Bild und drehe die Szene, dann bekommst Du einen räumlichen Eindruck. In der (grünen) YZ-Ebene befindet sich ein Vektor \(b\); er hat keine Ausdehnung in X-Richtung, folglich ist seine X-Koordinate =0. In diesem Bild ist
$$b = \begin{pmatrix} 0 \\ 2 \\ 1\end{pmatrix}$$ Jeder Vektor \(v_2\) in der YZ-Ebene hat die Koordinaten:$$v_2 = \begin{pmatrix} 0 \\ y \\ z\end{pmatrix}$$ Entsprechendes gilt für die beiden anderen Ebenen, für die jeweils eine andere Koordinate den Wert 0 hat.
Im nächsten Bild habe ich Dir die beiden Vektoren \(a\) und \(c\) eingezeichnet und die Ergebnisse für die drei Vektoren \(b_1\) bis \(b_3\).
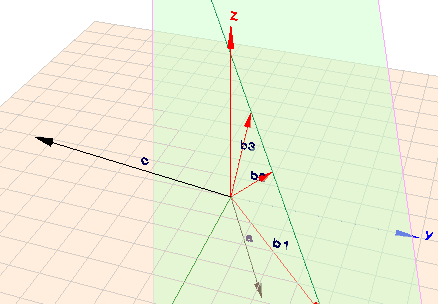
(klicke und drehe)
Um einen der Vektoren zu berechnen, stellen wir die beiden Bedingungen formal auf. (1. Bedingung) Der Vektor \(b_1\) liegt in der XY-Ebene und hat folglich die Koordinaten $$b_1 = \begin{pmatrix} x \\ y \\ 0\end{pmatrix}$$ und (2. Bedingung) \(b_1\) soll diese Gleichung \(c = a \times b_1\) erfüllen. Einsetzen der drei Vektoren \(c\), \(a\) und \(b_1\) gibt dann:
$$\begin{pmatrix} 4\\-4\\4 \end{pmatrix} = \begin{pmatrix} 3\\2\\-1 \end{pmatrix} \times \begin{pmatrix} x\\y\\ 0 \end{pmatrix} = \begin{pmatrix} y\\-x\\3y-2x \end{pmatrix} \quad \Rightarrow x=4; \space y=4$$ Folglich ist \(b_1 = \begin{pmatrix} 4 & 4 & 0\end{pmatrix}^T\). Wie Du siehst, stehen dort drei Gleichungen (in drei Zeilen) für nur zwei Unbekannte. Das geht nur deshalb immer auf, weil \(a\) und \(c\) bereits senkrecht zueinander stehen. Das gleiche mache ich jetzt für die beiden anderen Vektoren \(b_2\) und \(b_3\):
$$\begin{pmatrix} 4\\-4\\4 \end{pmatrix} = \begin{pmatrix} 3\\2\\-1 \end{pmatrix} \times \begin{pmatrix} 0\\y\\ z \end{pmatrix} = \begin{pmatrix} 2z-y\\-3z\\3y \end{pmatrix} \quad \Rightarrow y=\frac43; \space z=\frac43\\ \begin{pmatrix} 4\\-4\\4 \end{pmatrix} = \begin{pmatrix} 3\\2\\-1 \end{pmatrix} \times \begin{pmatrix} x\\0\\ z \end{pmatrix} = \begin{pmatrix} 2z\\-x-3z\\-2x \end{pmatrix} \quad \Rightarrow z=2; \space x=-2$$ Die Vektoren lauten also: \(b_2 = \begin{pmatrix} 0 & 4/3 & 4/3\end{pmatrix}^T\) und \(b_3=\begin{pmatrix} -2 & 0 & 2\end{pmatrix}^T\).
Ziehst Du zwei dieser Vektoren von einander ab
$$b_1 - b_2 = \begin{pmatrix} 4 \\ 4 \\ 0\end{pmatrix} - \begin{pmatrix} -2 \\ 0 \\ 2\end{pmatrix} = \begin{pmatrix} 6 \\ 4 \\ -2\end{pmatrix} = 2 \begin{pmatrix} 3 \\ 2 \\ -1\end{pmatrix} = 2a$$ so ist das Ergebnis ein Vielfaches von \(a\). Die Differenz zweier Vektoren von \(b\) und der Vektor \(a\) verlaufen demnach parallel.
Das liegt daran, weil die Spitzen aller Vektoren \(b\), die die Gleichung \(c=a \times b\) erfüllen, auf einer Gerraden liegen. Warum das so sein muss, darfst Du Dir selber überlegen. Tipp: schau mal wie man mit Hilfe des Kreuzprodukts die Fläche eines Parallelogramms berechnet.
Gruß Werner