Passendes Quadrat gesucht, Geometrie Hilfe!

Question

hallo. Ich habe Schwierigkeiten bei folgender Aufgabe. Aufjedenfall muss es etwas mit Zentrischer streckung und ähnlichkeit zu tun haben:

In einem beliebigen Dreieck ABC soll ein Quadrat so einbeschrieben werden, dass die eine Quadratseite auf AB liegt und die beiden weiteren Quadratseiten auf BC und AC. Hinweis: Variieren Sie mit dem TI-Nspire. Beginnen Sie mit einem beliebigen Quadrat und verändern Sie dieses.

Wie gesagt, Dreieck kann beliebig aussehen!

Comments

und die beiden weiteren Quadratseiten auf BC und AC

Gemeint ist wohl, dass die Ecken auf BC und auf AC liegen. Du würdest ansonsten Probleme mit den Winkeln bekommen. Die müssen in eine Quadrat 90° sein, in einem Dreieck kann es aber nur einen 90°-Winkel geben.

Answer 1

~draw~ dreieck(-10|0 10|-8 10|5){000};text(-10.6|0 "C"){000};text(10|-8.5 "A"){000};text(10|5.5 "B"){000};strecke(-10|0 10|0){000};text(10.3|0 "H"){000};rechteck(2|-4.8 8 7.8){040};text(1.8|-5.2 "P"){040};text(10.2|-5.2 "Q"){040};text(10.2|3.2 "R"){040};text(1.8|3.3 "S"){040};;punkt(2|0 "M");zoom(10);aus ~draw~

Die Strecken CH, PQ und SR stehen senkrecht auf AB.

Die Details, wie du das ausrechnest, hängen davon ab, welche Sträckenlängen bekannt sind.

Tipps:

• Die Dreiecke CMS, CHB und SRB sind ähnlich
  
• Die Dreiecke CPM, CAH und PAQ sind ähnlich.
• Es soll PS = PQ sein.
• Es ist PS = PM + MS = QH + HR
  

Answer 2

Beginnen Sie mit einem beliebigen Quadrat und verändern Sie dieses.

Ja - dann tue dies doch einfach. In der Skizze habe ich ein Dreieck gezeichnet und auf der Seite \(AC\) eine Punkt \(S_1\) gewählt, und das Lot auf die Seite \(AB\) gefällt. Dann hat man schon eine Seite eines Quadrats und kann dies jetzt zeichnen.

 

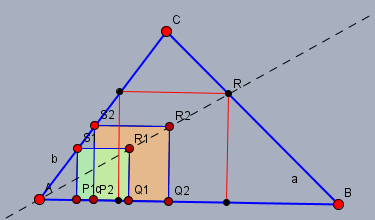
fertig ist das Quadrat \(P_1Q_1R_1S_1\) Falls Du nicht weißt, wie das geht - bitte melden. Wenn einem sonst nichts einfällt, kann man einen zweiten Punkt \(S_2\) auf \(AC\) wählen und diesen dann zu einem zweiten Quadrat \(P_2Q_2R_2S_2\) ergänzen.

Auf jeden Fall muss es etwas mit Zentrischer Streckung und Ähnlichkeit zu tun haben

Guter Tipp. Schau Dir die beiden entstandenen Quadrate an. Beide können durch eine Streckung - mit Zentrum in \(A\) - in einander überführt werden. D.h. egal wo man den Punkt \(S_1\) auf \(AC\) hin setzt, der zugehörige Punkt \(R_1\) wird immer auf einer Geraden liegen, die durch \(A\) geht (schwarz gestrichelt). Es reicht also ein beliebiges Quadrat zu zeichnen, für eine Punkt \(R_1\), eine Gerade durch \(A\) und \(R_1\) zu legen und der Schnittpunkt dieser Geraden mit der Seite \(BC\) ist dann der gesuchte Punkt \(R\).

Jetzt ausgehend von \(R\) das gesuchte Quadrat konstruieren. Falls etwas nicht klar ist, so melde Dich bitte.

Gruß Werner