Hallo Mara,
zur Klärung der Bezeichnungen spielt die besondere Rechteckform keine Rolle:
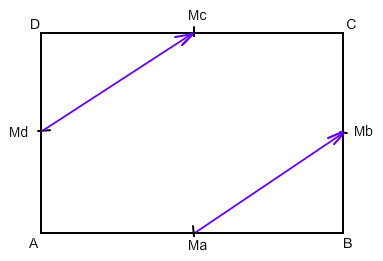
Ohne Bezug auf die besondere Rechteckform in der Zeichnung gilt:
Der Orsvektor \(\vec{m}\) des Mittelpunkts einer Strecke XY ist gleich 1/2·(\(\vec{x}\) + \(\vec{y}\))
\(\color{blue}{\overrightarrow{M_aM_b}}\) = \(\vec{m}_b\) - \(\vec{m}_a\) = 1/2 · ( \(\vec{b}\) + \(\vec{c}\)) - 1/2 · (\(\vec{a}\) + \(\vec{b}\)) = 1/2 · (\(\color{blue}{\vec{c} - \vec{a}}\))
\(\color{blue}{\overrightarrow{M_dM_c}}\) = \(\vec{m}_c\) - \(\vec{m}_d\) = 1/2 · (\(\vec{c}\) + \(\vec{d}\)) - 1/2 · (\(\vec{a}\) + \(\vec{d}\)) = 1/2 · (\(\color{blue}{\vec{c} - \vec{a}}\))
Gruß Wolfgang