Hallo Mary,
... Polarkoordinaten und was sind die überhaupt?
Mal angenommen, Du sitzt in einer Radarstation am Meer und in der Nähe befindet sich ein Schiff. Ein Radar ist eine Antenne, die ein Radiosignal in eine Richtung sendet.
Dies Signal wird ggf. von einem Gegenstand reflektiert und das Echo wird wieder vom Radar empfangen. Nun ist die Richtung (bzw. der Winkel \(\varphi\)) bekannt, aus der das Signal kommt, und aus der Laufzeit des Echos kann man auf die Entfernung \(r\) des Gegenstands schließen.

Oben im Bild ist \(\varphi=-60°\) (minus 60, da der blaue Winkel mathematisch negativ zur horizontalen Achse dreht) und die Entfernung ist \(r=1\text{km}\). Und schon haben wir die Polarkoordinaten \(p_S\) des Schiffes bezogen auf die Radarstation:$$p_S = (r=1\text{km}|\, \varphi=-60°)$$
Um den Zusammenhang zwischen Polar- und kartesischen Koordinaten zu klären betrachte bitte folgendes Bild:
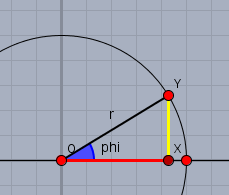
Die Punkte \(O\), \(X\) und \(Y\) bilden ein rechtwinkliges Dreieck. Der Winkel bei \(O\) (blau) sei \(\varphi\) und die Strecke \(|OY|=r\). Die kartesischen Koordinaten des Punktes \(Y\) sind \(x=|OX|\) (rot) und \(y=|XY|\) (gelb). Und nach der Definition der trigonometrischen Funktionen ist:$$x = r \cdot \cos \varphi \\ y = r \cdot \sin \varphi$$ oder umgekehrt folgt aus Pythagoras und \(\tan \varphi = y/x\):$$r = \sqrt{x^2 + y^2} \\ \varphi = \arctan \frac{y}{x}$$
In Deinem Fall ist \(x=\frac 12 \) und \(y= -\frac12 \sqrt 3\). Einsetzen in die Gleichungen für \(\varphi\) und \(r\) gibt:$$\begin{aligned}r &= \sqrt{x^2 + y^2} \\ &= \sqrt{\left( \frac 12\right)^2 + \left( -\frac 12 \sqrt 3\right)^2} \\&= \sqrt{ \frac 14 + \frac 14 \cdot 3} \\&= \sqrt {\frac 44} = 1\end{aligned}$$und für den Winkel:$$\begin{aligned}\varphi &= \arctan \left( \frac yx\right) \\&= \arctan \left( \frac {-\frac 12 \sqrt 3}{ \frac 12}\right) \\&= \arctan \left( -\sqrt 3\right) = -60°\end{aligned}$$ Falls etwas unklar ist, so frage bitte nach.
Gruß Werner