f(x) = x^4 - k·x^2
f'(x) = 4·x^3 - 2·k·x
f''(x) = 12·x^2 - 2·k
Extremstellen f'(x) = 0
4·x^3 - 2·k·x = 0
k = 2·x^2
Ortskurve aller Extrempunkte
g(x) = x^4 - (2·x^2)·x^2 = -x^4
Wendestellen f''(x) = 0
12·x^2 - 2·k = 0
k = 6·x^2
Ortskurve aller Wendepunkte
g(x) = x^4 - (6·x^2)·x^2 = - 5·x^4
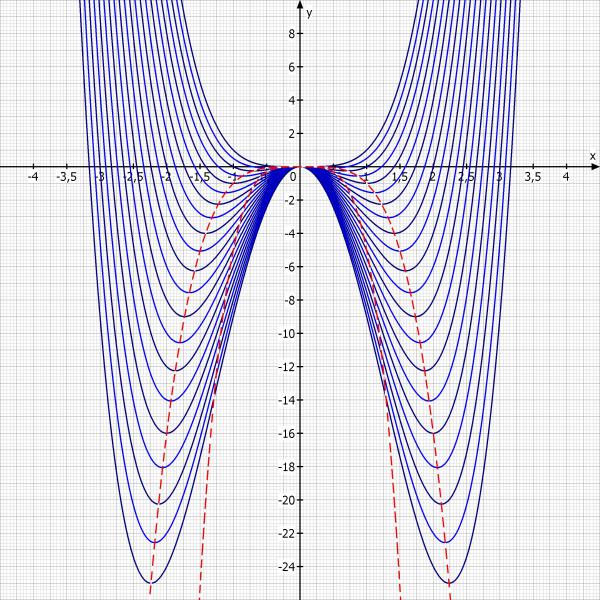
Skizze: