Ist die Pyramide regelmäßig, so gilt das auch für ihre Grundfläche. Die ist also ein regelmäßiges - d.h. gleichseitiges Dreieck mit der Kantenlänge \(a=17,6 \text{cm}\). Die Höhe(n) \(h_D\) in diesem Dreieck lässt sich über den Pythagoras berechnen. Es gilt:$$a^2 = \left( \frac a2 \right)^2 + h_D^2\\ \implies h_D = \sqrt{a^2 -\left( \frac a2 \right)^2 } = a \sqrt {1 - \frac 14} = \frac a2 \sqrt 3 \approx 15,24\, \text{cm}$$In einem gleichseitigen Dreieck ist die Höhe gleichzeitig auch Seitenhalbierende. Die Spitze der Pyramide soll senkrecht oberhalb des Schwerpunkts liegen. Also bilden die Höhe \(h=|OS|\) der Pyramide eine Kante \(s\) und \(2/3\) von \(h_D\) rechtwinkliges Dreieck \(\triangle AOS\) (blau).
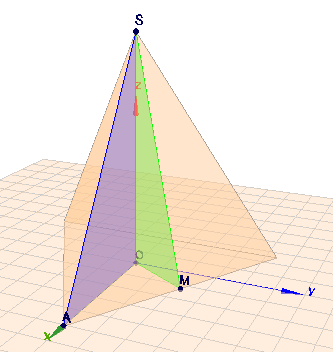
(klick auf das Bild) Es gilt wieder der Pythagoras:$$s^2 = h^2 + \left( \frac 23 h_D \right)^2 \\ \implies h = \sqrt{s^2 - \frac 49 \cdot \frac 34 a^2} = \sqrt{s^2 - \frac 13 a^2} \approx 15,70\, \text{cm}$$Das Volumen \(V\) der Pyramide mit Höhe \(h\) und Grundfläche \(G\) ist$$V = \frac 13 h \cdot G = \frac 13 h \cdot \frac 12 ah_D \approx 701,8\, \text{cm}^3$$Zur Berechnung der Oberfläche ist noch die Höhe \(h_S= |MS|\) einer Seitenfläche zu berechnen. Das geht wieder über den Pythagoras ... -> \(\triangle AMS\)
Kommst Du allein klar? Sonst frage bitte noch mal nach.
Gruß Werner