Alles was wir von der Aufgabestellung wissen, fasse ich mal hier zusammen:
Das gleichseitige Dreieck \(\triangle ABD\) bildet die Grundfläche einer geraden Pyramide mit Spitze in \(Q\). Der Schwerpunkt des Dreiecks sei \(P_S\). Die Koordinaten von \(Q\), \(D\) und \(P_S\) sollen sein:$$Q = \begin{pmatrix} 4\\1\\6 \end{pmatrix}, \quad D = \begin{pmatrix} 3\\ -1\\ 2 \end{pmatrix}, \quad P_S = \begin{pmatrix} 1\\ 1\\ 2 \end{pmatrix}$$ Sowie der Abstand \(|QP_S|\)$$|QP_S|=5$$Jetzt habe wir schon festgestellt, dass das in sich widersprüchlich ist (s. Kommentare bei der Frage)! Der Abstand und die Koordinaten passen zueinander, ich gehe also davon aus, dass der Fehler in der Aufgabenstellung beim Punkt \(D\) liegt. Ich nehme daher an, dass$$D = \begin{pmatrix} \colorbox{#F00}1\\ -1\\ 2 \end{pmatrix}$$D.h. die X-Koordinate von \(D\) ist nicht 3 sondern 1!
Ermitteln Sie die Maßzahl des Flächeninhaltes der Grundfläche ABD dieser Pyramide
In einem gleichseitigen Dreiecks fallen Höhen und Seitenhalbierende zusammen. Sei \(h\) die Höhe im Dreieck, so ist die Entfernung eines Eckpunktes zum Schwerpunkt $$|DP_S| = \frac 23 h = 2$$Die Höhe \(h\) steht in Beziehung zur Seite \(a\)$$h=\frac 12 \sqrt 3\, a \implies a = |DP_S| \cdot \sqrt 3 = 2\sqrt 3$$Die Fläche des Dreiecks ist also$$A=\frac 12 ah = \frac 12 \cdot (2\sqrt 3) \cdot \left( \frac 12 \sqrt 3\, \cdot 2\sqrt 3 \right) =3 \sqrt 3 \approx 5,196 $$
Bestimmen Sie die Koordinaten des Mittelpunktes der Seite [AB].
Durch die Position des Schwerpunkts \(P_S\) der Grundfläche ist die Lage der Pyramide fest gelegt.
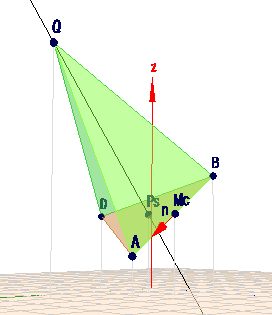 (klick auf das Bild)
(klick auf das Bild)
Daraus berechnet man den Punkt \(M_c\) - den Mittelpunkt der Seite \(AB\). Es ist $$M_c= D + \frac 32 \vec{DP_S} = \begin{pmatrix} 1\\ 2\\ 2\end{pmatrix}$$
Und zuletzt noch die Koordinaten von \(A\) und \(B\), nach denen in der Aufgabe gar nicht gefragt wurde!
Die Grundfläche steht senkrecht auf \(QP_S\). Die Seite \(AB\) steht senkrecht auf \(DP_S\). Somit lässt sich der Einheitsvektor \(n\) in Richtung von \(AB\) aus dem Kreuzprodukt von zwei Vektoren in der Ebene der Punkte \(DQP_S\) berechnen$$n = \frac{\vec{QP_S} \times \vec{DP_S}}{\left|\vec{QP_S} \times \vec{DP_S}\right|} = \frac 15 \begin{pmatrix} 4\\ 0\\ -3 \end{pmatrix}$$Da die Seite \(a\) bereits bekannt ist, kommt man nun direkt zu den Punkte \(A\) und \(B\)$$A = M_c + n \cdot \frac a2 \approx \begin{pmatrix}2.386\\ 2\\ 0.961 \end{pmatrix} \\ B = M_c - n \cdot \frac a2 \approx \begin{pmatrix}-0.386\\ 2\\ 3.039 \end{pmatrix}$$Falls Du noch Fragen hast oder sich die Aufgabenstellung noch mal ändert, so melde Dich ruhig noch mal
Gruß Werner