Question

Lösen sie zeichnerisch folgende Ungleichung: 2 ≤ |x-2| < 6

Aufgabe: Oben steht bereits die Aufgabe. Meine Frage ist nun, ob dies Richtig so ist, oder ein Fehler  zu finden ist

Comments

Lösungsmenge sind die Zahlen von -4 bis 0 und von 4 bis 8.

Answer 1

Meine Frage ist nun, ob dies Richtig so ist, oder ein Fehler  zu finden ist

Du hast y = - 2 gezeichnet anstelle von y = 2.

Daher musst du in der Mitte der Lösungsmenge noch etwas entfernen.

Ausserdem solltest du das Resultat am Schluss bestimmt auch noch als Menge beschreiben. Z.B. so:

L = { x Element R | -4 < x ≤ 0 oder 4 ≤ x < 8 } 

Comments

supii, danke !!

---

Bitte. Gern geschehen !

Answer 2

2 ≤ | x - 2 |
6 > | x - 2 |
Beides muß stimmen

x - 2 = 0
x = 2

Für x ≥ 2 gilt

2 ≤ | x - 2 |
2 ≤  x - 2
x ≥ 4

6 > | x - 2 |
6 > x - 2
x < 8

4 ≤ x < 8

Für x < 2 gilt

2 ≤ | x - 2 |
2 ≤  (-1) * ( x - 2 )
2 ≤  - x + 2
x  ≤ 0

6 > | x - 2 |
6 > ( -1 ) * ( x - 2 )
6 > - x + 2
x >  -4

- 4 ≤ x < 0

Zusammen
( 4 ≤ x < 8 ) und ( - 4 ≤ x < 0 )

Ich frage mich nur noch wie ich das
zeichnerisch lösen kann.

Comments

wäre dies so richtig? Habe die Zeichnung aus ner Lösung übernommen und die Rechnung  von hier übernommen und angepasst :)

---

Rechnerisch geht es noch einfacher
2 ≤ | x - 2 |  < 6

für x ≥ 2 gilt
2 ≤ x - 2   < 6   | + 2
4  ≤ x < 8

für x < 2 gilt
2 ≤ (-1) * ( x - 2 ) < 6
2 ≤  - x + 2  < 6  | - 2
0  ≤  - x  < 4  | * -1
0  >  x  > -4
-4 < x < 0

( -4 < x < 0) und ( 4  ≤ x < 8 )

---

2 ≤ |x-2| < 6
teilen wir einmal auf
2 ≤ |x-2|
|x-2| < 6

0 ≤ |x-2| - 2
0 > |x-2| - 6

Als Grenzgerade
0 = |x-2| - 2
0 = |x-2| - 6

Als Funktion
f ( x ) = |x-2| - 2 ( blau )
g ( x)  = |x-2| - 6 ( rot )

Die Graphen

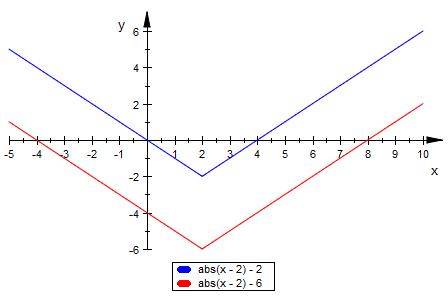
blau
0 ≤ |x-2| - 2
Null ist kleiner |x-2| - 2
Zwischen ( -∞ und 0 ) und ( 4 .. ∞ )

rot
0 > |x-2| - 6
Null ist größer als |x-2| - 6
Zwischen -4 und 8

Darstellung auf dem Zahlenstrahl

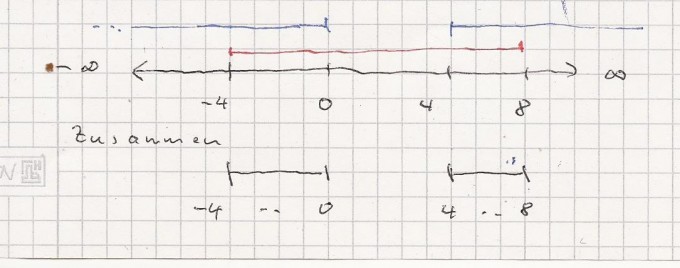
mfg Georg

---

Eigentlich ist es einfach
2 ≤ | x - 2 |  < 6
es gilt nur die Funktion
| x - 2 |  zu zeichnen.

Wertetabelle für x - 2
x | y
2 | 0
2. Punkt auf der Geraden
x = 5 | y = 3
Gerade ( 2 | 0 )( 5 | 3 ) Punkte verbinden
Wertetabelle für (-1) * ( x - 2) = -x + 2
( 2 | 0 )
2. Punkt auf der Geraden
x = -5 | y = 7
Gerade ( 2 | 0 )( -5 | 7 ) Punkte verbinden
Dann noch
y =2 und y = 6 einzeichen.
Siehe Skizze Mathecoach.

---

1 < | x + 0.5 | ≤ 2
zeichnerische Lösung
Die Funktion | x + 0.5 | zeichnen
dann
y = 1
und
y = 2
einzeichnen

( -2.5 ≤ x < -1.5 ) und ( 0.5 < x ≤ 1.5 )

---

@georgborn danke dir nochmals,

---

Gern geschehen.
Dazu ist das Forum da.

Answer 3

2 ≤ |x - 2| < 6 --> -4 < x ≤ 0 ∨ 4 ≤ x < 8 → L = ]-4 ; 0] ∪ [4 ; 8[

Ich würde es wie folgt zeichnen

~plot~ abs(x-2);2;6;[[-6|10|-2|10]] ~plot~

Comments

ich habe ne Neue Aufgabe angefangen, wäre dies so richtig, um die Aufgabe zu lösen?  :)

Danke schonmal für die hilfe

---

Da sind noch etliche Fehler drin. Du solltest dazu schreiben welchen Fall du untersuchst. weiterhin solltest du das/die Ungleichheitszeichen bei Multiplikation mit einer negativen Zahl tauschen. Und als letztes solltest du Teillösungen zu einer Lösung zusammenfassen.

Du solltest am Ende rechnerisch auf die Lösung kommen

1 < |x + 0.5| ≤ 2 --> -2.5 ≤ x < -1.5 oder 0.5 < x ≤ 1.5

---

So richtig?

Dir auch nochmals danke !

Aber wieso ändert sich das Vorzeichen von -1.5 und das von -2.5 nicht? :\

---

Die Fälle sind
x >= -0.5  oder  x < -0.5

ein < wird zu > und nicht zu >= ein >= wird zu <= und nicht zu <.

---

Ich habs jetzt verstanden, danke ! :)

---

Zum kontrolle, wäre 0< |5-2x|<=7

2.5>x>=-1    und 2.5<x<=6

oder vertue ich mich da wieder?? Ein ja oder nein genügt, da ich selbst auf die Lösung kommen will :)

---

Ja. kann man aber auch noch zusammenfügen
-1 < x < 6

---

Supi, danke :)