Aufgabe:
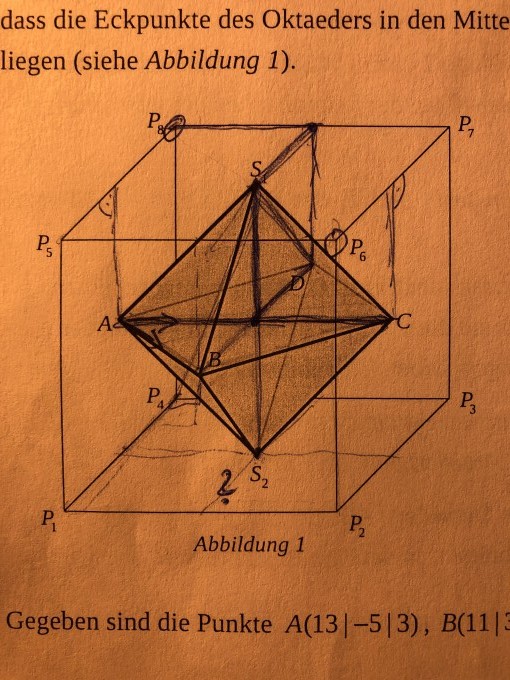
[...] Nun werden von allen Ecken des Oktaeders ABCDS1S2 gleich große Pyramiden mit der Kantenlänge k abgeschnitten, sodass ein Restkörper Rk entsteht.
Beschreiben Sie diesen Restkörper Rk für den Fall k = \( \frac{1}{3} \) \( \cdot \) | \( \vec{AS_{1}} \)| hinsichtlich der Anzahl und Eigenschaften seiner Seitenflächen (Anzahl der Ecken, Seitenlängen).
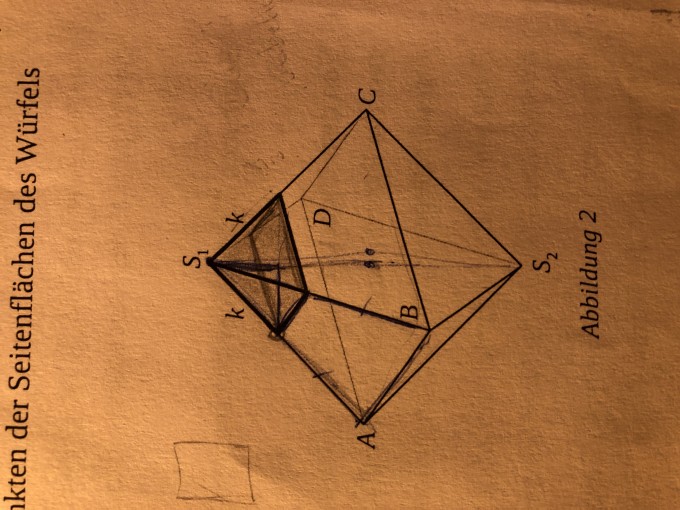
Meine Frage ist eigentlich nur, was mit „Seitenlängen“ gemeint ist. Ist die Fläche des Quadrats gemeint, oder die des Trapezes?
Anzahl der Ecken müsste ja einfach 24 sein, oder?