Berechnen des Urbildes von Intervallen einer Funktion f

Question

Aufgabe:

Gegeben sei die Funktion f: ℝ→ℝ, f(x)=x³-2x.

a) Skizzieren Sie den Graphen der Funktion und kennzeichnenn Sie das Bild des Intervalls [1,2] unter f.

b) Berechnen Sie das Urbild der Intervalle (0,∞) und [0,∞). Bestimmen Sie außerdem zeichnerisch das Urbild von [((-4·√2)/(3·√3)),((4·√2)/(3·√3))] unter f.

Problem/Ansatz:

Ich bin neu an der Uni (komme gerade aus der Schule) und bin mit Abbildungen und Urbildern usw. nicht wirklich vertraut...Aus den Vorlesungen weiß ich, was das ist, jedoch nicht wie man das ganze formal korrekt beantwortet. Wäre super, wenn mir jemand helfen könnte.

Answer 1

zu a)

erst einmal zeichnen;

https://www.desmos.com/calculator/l5occu7hdb

Der Kurvenabschnitt im x-Intervall [1;2] ist farbig hervorgehoben. Die Funktionswerte gehen von y=-1 bis y=4. Das Bild des Intervalls ist also [-1;4] auf der y-Achse. (Hier nicht eingezeichnet.)

zu b)

Das Intervall mit den Wurzeln sind die y-Werte zwischen den Extrema, also zwischen den rot gestrichelten Linien. Das Urbild dieses Intervalls findest du, indem du guckst, welche x-Werte dazu gehören. Aus dem Desmos-Graphen lese ich die gerundeten Werte [-1,633;+1,633] ab. Da die Aufgabe zeichnerisch gelöst werden soll, reicht diese Genauigkeit.

Nun zur Berechnung des Urbildes von (0;∞)

Gesucht sind die x-Werte, für die gilt: f(x)>0.

f(x)=x³-2x=x·(x²-2)

Damit ein Produkt positiv ist, müssen beide Faktoren gleiches Vorzeichen haben.

1. Fall:  x>0 und x²-2>0 führt zu \(x>\sqrt{2}\)

2. Fall:  x<0 und x²-2<0 führt zu \(-\sqrt{2}<x<0\)

Das stimmt mit der zeichnerischen Lösung überein, da in diesen x-Intervallen die Kurve oberhalb der x-Achse verläuft.

Answer 2

f(x)=x³-2x=x(x²-2)=x(x-√2)(x+√2) Damit ist die Skizze klar.

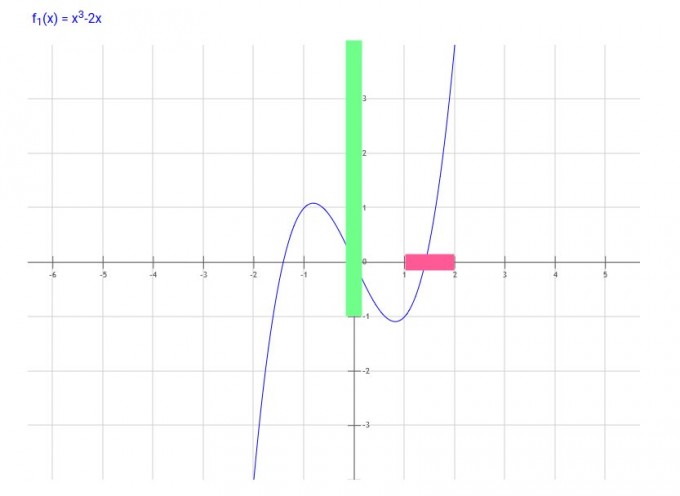
rot sind die x-Werte, das Urbild, das Intervall [1,2]

grün sind die von diesen x-Werten erreichten y-Werte, das Bild von [1,2], nämlich [-1,4]

Berechnen Sie das Urbild der Intervalle (0,∞), d.h. welche x-Werte haben y-Werte in (0,∞): die roten:

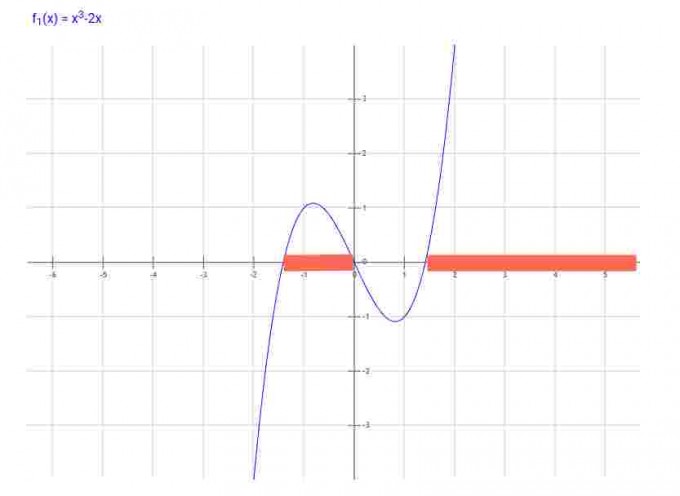
genau: (√2,∞) ∪ (-√2,0)  Die Grenzen sind ausgeschlossen.

Berechnen Sie das Urbild der Intervalle [0,∞): Wieder mit der Faktorzerlegung ganz oben, y=0 ist diesmal drin:

[√2,∞) ∪ [-√2,0)  Die √ sind eingeschlossen.

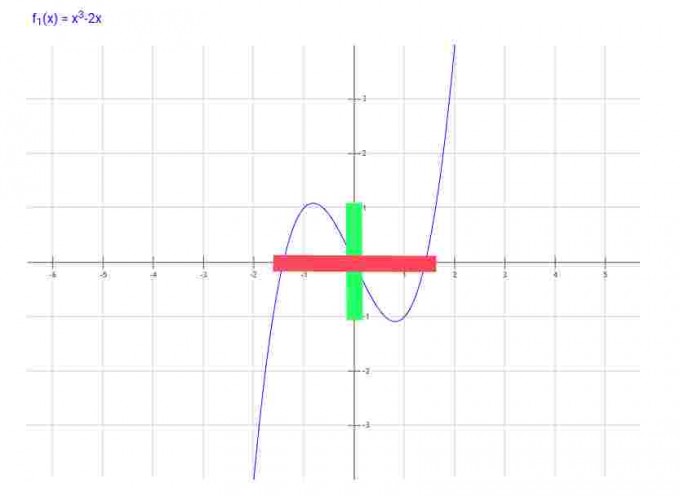
Bestimmen Sie außerdem zeichnerisch das Urbild von [((-4·√2)/(3·√3)),((4·√2)/(3·√3))]

Das sind wohl die y-Werte des H und T. Das Urbild geht also vom x-Wert von H bis zum x-Wert von T, aber auch noch von den anderen x-Werten die y-Werte in [((-4·√2)/(3·√3)),((4·√2)/(3·√3))]  haben, also rot: [-1,7;1,7]