Bestimmung von Funktionschare ft und Funktionsgleichung der Ortskurve

Question

Aufgabe:

Bestimmen Sie für die Funktionsschare ft mit t ungleich 0 die Extrempunkte ,sowie die Funktionsgleichung der zugehörigen Ortskurven.

a.ft (x)= x^2 + tx +2

b. ft(x)=t^3x^2+t^2x+t

Problem/Ansatz:

Möchte wissen ,ob meine Ergebnisse richtig sind ?

Comments

b)   2t³ > 0  , da t≠0   , somit .... Tiefpunkt

Das trifft für negative t nicht zu.

Answer 1

Extrempunkte

f(x) = t^3·x^2 + t^2·x + t

f'(x) = 2·t^3·x + t^2 = 0 --> x = - 1/(2·t)

f(-1/(2·t)) = 0.75·t

Für t > 0 ist TP(-1/(2·t) | 0.75·t)

Für t < 0 ist HP(-1/(2·t) | 0.75·t)

Ortskurve der Extrempunkte

2·t^3·x + t^2 = 0 --> t = -1/(2·x) (∨ t = 0)

y = (-1/(2·x))^3·x^2 + (-1/(2·x))^2·x + (-1/(2·x)) = -3/(8·x)

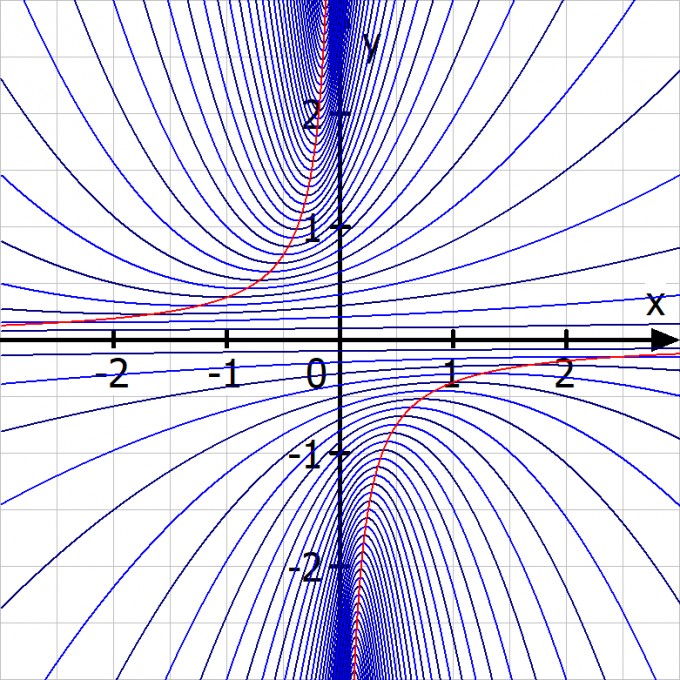
Skizze