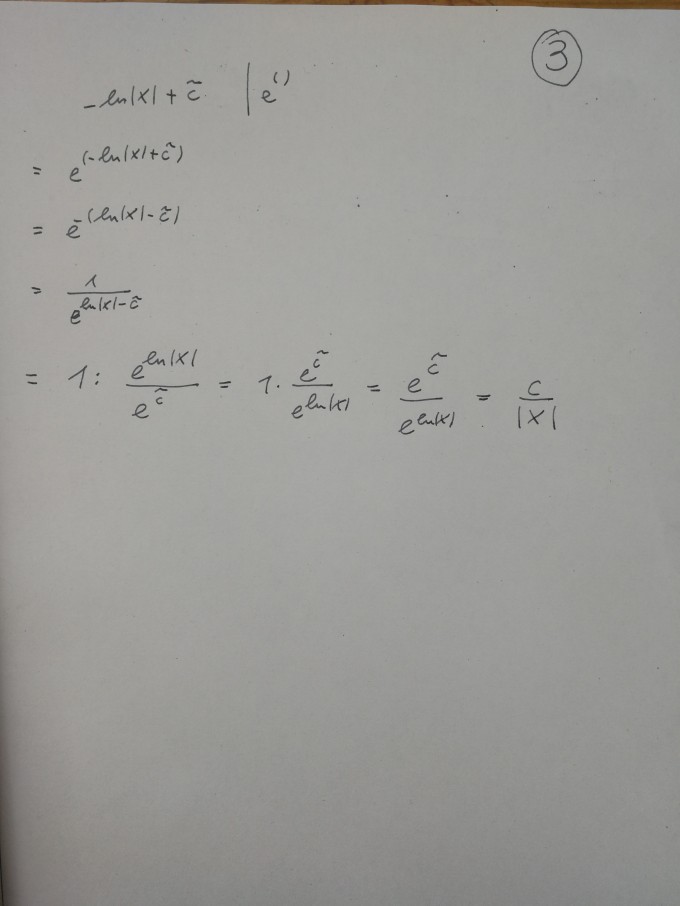Differentialgleichung: y'+(1/x)*y = 1+x , y(1)=0

Question

Aufgabe:

Die Aufgabe steht im Titel.

Problem/Ansatz:

Diese Aufgabe haben wir in der Vorlesung gerechnet. Der Zettel mit der roten Schrift ist die Mitschrift der Vorlesung.

Ich verstehe nicht wie der Dozent auf  die Lösung der homogenen DGL kommt. Insbesondere verstehe ich nicht den Ansatz mit y1(x), wo im Argument der e-Funktion das Integral steht.

Warum macht er das so? Und wann macht man das so? (Die Lösung ist yh(x) = C/x)

Ich habe die Aufgabe dann so gerechnet wie ich das kenne, (zweites Blatt)

Ich komme auf yh(x) = 1/(C*x)

Das ist ja anders als die richtige Lösung. Was habe ich falsch gemacht?

Ich vermute mal ich habe die rechte Seite falsch umgeformt?

Ich habe dann auf dem 3.ten Blatt die rechte Seite nochmal anders umgeformt. Dann komme ich auch auf yh(x)=C/x

Ist meine Umformung auf dem 3.ten Blatt korrekt? Wenn ja welcher Weg ist der richtige/bessere die DGL zu lösen?

 

Answer 1

Das ist schon beides das Gleiche:

yh(x) = C/x

Und :   yh(x) = 1/(C*x) = 1/c *  1/x und mit D=1/C also  yh(x) = D/x

Answer 2

Es geht hier um "Variation der Konstanten"

Der Dozent hat die DGL mittels Lösungsformel berechnet (sollte in Deinen Unterlagen stehen)

Man kann diese DGL auch nach Deinem Weg rechnen.(Berechnung der homogenen DGL usw.)

Welcher Weg ist egal. Du mußt es so machen , wie der Dozent es will , sonst gibt es Punktabzug.

1/c = K kann Du als neue Konstante festlegen ,das Ergebnis ist richtig.