Wie groß ist das Volumen dieses Zylinders?

Question

Aufgabe:

Einem Drehkegel mit dem Radius \( r=6 \mathrm{cm} \) und der Höhe \( h=12 \mathrm{cm} \) ist der volums größte Drehzylinder einzuschreiben (Achsenschnitt abgebildet).

Wie groß ist das Volumen dieses Zylinders?

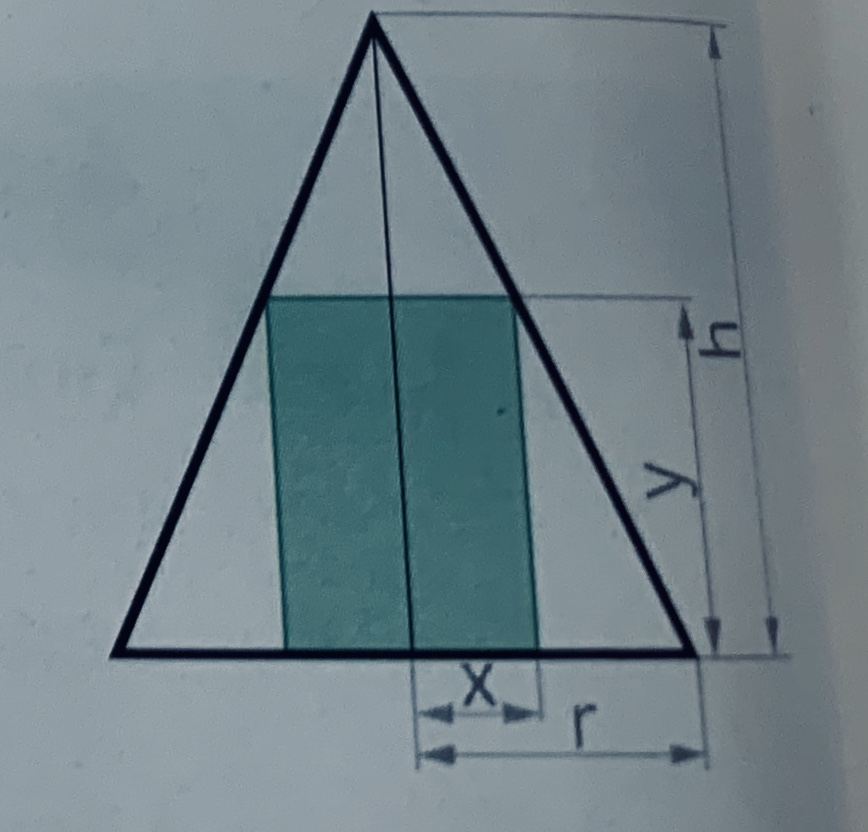
Problem/Ansatz:

Mein Ansatz war y:(r-x)=h:r, aber ich komme nicht auf das Ergebnis lt. Lösungsheft: V=64*pi~201,1cm^3...

Answer 1

\(y=-2x+12\) beschreibt die Mantellinie, wenn der Ursprung eines Koordinatensystems in den Mittelpunkt der Grundfläche gelegt wird.

Volumen des Zylinders:

\(V=\pi x^2 y \Rightarrow V(x)=\pi x^2 (-2x+12)\)

Ableiten, Null setzen usw.

...

\(x=4, y=4, V=64\pi\)

Comments

Warum ist die Steigung hier -2?

---

12 nach unten, 6 nach rechts → m=-12/6=-2