Berechnung von Kreisen und Kreisteilen.

Question

Ich bräuchte für folgende Aufgabe eure Hilfestellung. Es geht um die Berechnung der grau schraffierten Fläche in der unteren Figur. Die Seitenlänge des Quadrates ist 2 Einheiten lang.

Mein Problem ist gerade, dass ich zu kompliziert denke. Ich kann es zwar ausrechnen, allerdings nur unter Verwendung der Trigonometrie. Die ist aber in Klasse 9 noch nicht bekannt.

Es wäre nett, wenn mir jemand auf die Sprünge helfen könnte.

Comments

Mit dem Pythagoras kann ich mir ausrechnen wo mein Kreisbogen, die Mittelsenkrechte über der unteren Quadratseite schneidet.

h = Wurzel(2^2 - 1^2) = Wurzel(3)

Das ist kein Thema. 9 Klasse hatte ja den Pythagoras.

 

 

Also ich habe es so berechnet das ich die Hälfte einer weißen Fläche berechnet habe.

Dazu nehme ich z.B. die linke Quadrathälfte (1 * 2) und subtrahiere davon ein Kreissektor mit dem Innenwinkel von 30 Grad (Den Innenwinkel bekomme ich über den Sinus) und subtrahiere das Dreieck mit der Höhe von Wurzel(3).

w = 1 * 2 - pi * 2^2 * 30/360 - 1/2 * 1 * Wurzel(3) = -pi/3 - √3/2 + 2

Die gesamte Fläche kann ich jetzt berechnen indem ich von der Quadratfläche 8 mal die weiße Halbfläche abziehe.

A = 2^2 - 8 * (-pi/3 - √3/2 + 2) = 8·pi/3 + 4·√3 - 12 = 3,305783639

Das einzige Problem das ich habe zu erklären, wie ich auf den Kreissektor von 30 Grad gekommen bis. Also mit der Trigonometrie ist das kein Problem. Wie gesagt ist das aber erst Stoff von Ende der 9. Klasse und steht dem Schüler zum jetzigen Zeitpunkt noch nicht zur Verfügung.

Es würde mir also auch helfen, wie man erklären kann, das der Kreissektor 30 Grad hat ohne den Sinus zu benutzen. Aber da fällt mir nichts ein.

---

ich such ´ne Seite wo genau beschrieben wird wie man kreisteile berechnet. Ist diese Seite gut?

Answer 1

Du kannst F = a^2 - 8 A berechnen.

Die hellgrünen Kurven sollten Kreisbogen sein. Radius a. In der Mitte ein gleichseitiges Dreieck. Die Hälfte davon ist rot eingezeichnet.

A = a^2/2  - Pi a^2/12  - 1/2*a/2 √(a^2 - (a/2)^2)

A vereinfachen und dann in F einsetzen.

Comments

Ja. Das ist ja genau mein Lösungsansatz den ich oben im Kommentar hingeschrieben habe.

Mein Problem ist dabei wie man mit dem Stoff der 9. Klasse auf den Winkel von 30 Grad kommt. Klar kann ich dafür die trigonometrischen Funktionen benutzen. Aber das hatten die zu dem Zeitpunkt noch nicht in der 9. Klasse.

Trotzdem danke für deine Mühe. Auch wenn die Lösung hier bereits stand.

---

Das gleichseitiege Dreieck hat einen 60° Winkel

Das Quadrat einen rechten Winkel

Deshalb ist der rote automatisch 30° = 90° -60°

---

Oh ja danke. Das ist die Begründung, die mir gefehlt hat.

Answer 2

 Gegeben a= 2

Neben des Flächeninhaltes des Quadratges A= a² muss man wahrscheinlich  den Kreissektor  mit Hilfe der Bogelänge berechnen.

Bogenlänge

b= (d*π*α)/360                 α=90°        und d=2a  da  a =r die Seitenlänge des Quadrates ist und

                                                           damith  ist  2*r=d

b=(dπ*90)/360=d*π/4                   d=2a

b=aπ/2

dann ist die Fläche eines Viertelkreises

A= b*d/4                                    b und d einsezten

A=a*π*2a/4

A=a²*π/2                                     a=2

A=4π/2=2π    das wäre dann der Flächeninalt  des Kreisbogens im Quadrat mit der Längeneinheit 2.

davon dan die Hälfte der Flächen ds Quadrates abziehen.

A= 2π-2 und man erhält  dies es Flächenabschnitt

Das wiederum mal 2

A= 2(2π-2)         und dann erhält man folgende Fläche

So nun muss dann noch die uberschneidungsfläche  zweier solcher Flächen berechnen.

Dann ist die schraffierte Fläche

2*(4π-4)- Schnittfläche

 

 

Comments

Danke für die Mühe, aber es geht um das ausrechnen einer Fläche. Da kann ich ja nicht einfach sagen das ich die Schnittfläche deren Inhalt ich nicht kenne abziehe.

Es geht mir eigentlich auch weniger darum die Fläche auszurechnen. Die kenne ich und habe ich auch ausgerechnet. Meine Lösung habe ich jetzt mal im Kommentar angefügt.

Mein Problem ist eher, dass es eine Aufgabe eines Schülers der 9. Klasse ist und auch aus dem Mathebuch der 9. Klasse stammt und zu dem Zeitpunkt noch nicht bekannt ist wie man Winkel mit der Trigonometrie berechnet.

---

Meine Antwort war ja nicht so ganz zufriedenstellend veilleicht die nächste Skiuzze weiter

---

Naja. Das die roten Linien den den rechten winkel in genau 3 gleiche Teile teilen weiß ich ja. Aber das wäre ja eben zu zeigen. Und zwar ohne trigonometrische Funktionen mit allen Mitteln bis zur 9. Klasse.

Answer 3

Ich möchte mal eine nützliche Notation einführen: ich nenne die weißen Flächenstücken w, die grauen Außenstücke g und das Mittelstück m.
Jetzt muss man versuchen, ein Gleichungssystem mit möglichst vielen linear unabhängigen Informationen zu gewinnen, um daraus schließlich soviele Variablen zu eliminieren, dass man wenigstens eins der Flächenstücke wirklich ausrechnen kann.

Ein Viertelkreis hat die Fläche πr²/4 = π, also gilt:

π = m + 3g + 2w

Die ganze Fläche hat den Flächeninhalt 4:

4 = m+4g + 4w

Daraus lässt sich wenn man zwei Viertelkreise minus die ganze Fläche rechnet gewinnen:

2π-4 = m+2g

was Akelei schon ausgerechnet hat.

Alternativ kann man auch noch ausrechnen, wie man die anderen Variablen aus den ersten beiden Gleichungen eliminiert, das gibt aber keine weiteren Informationen!

4-π = g+2w  (das ist die Komplementärfläche eines Kreisviertels)

4π-12 = m-4w

 

Ich bin der Meinung, dass es mit einfachen Mitteln keine Möglichkeit gibt, noch mehr Informationen zu finden.

Man kann aber zum Beispiel die weiße Fläche mit Hilfe eines Integrals ausrechnen:
Und zwar folgendermaßen:

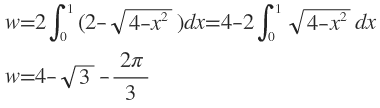
Das zweite Integral kann man durch partielle Integration und danach Substitution mit nem Sinus ausrechnen, will ich aber nicht machen, weil das vermutlich sowieso nicht die Lösung ist, die du suchst.

Zumindest kann man damit jetzt die gesuchte Größe ausrechnen, weil ja:

x = m+4g = 4-4w = 4√3+8π/3 - 12 ≈ 3.306

 

Wie man das mit einfachen Mitteln ausrechnen soll weiß ich nicht. Zumal da ja irgendwie die √3 reinkommen muss und ich sehe nicht wirklich, wo die herkommen soll.

Comments

Ja. Dein Ergebnis ist richtig. Das habe ich auch heraus. Meine Rechnung habe ich oben mal angefügt. Wie gesagt liegt eigentlich nicht mein Problem darin es auszurechnen. Das geht eigentlich sogar recht einfach. Mein Problem ist es ohne die Trigonometrie zu schaffen mit der ich den Innenwinkel einen Kreissektors berechnen kann.

Integralrechnung scheidet natürlich in der 9. Klasse auch aus :)

Wie gesagt habe ich oben im Kommentar zur Aufgabe mal meinen Rechenweg aufgezeigt. Vielleicht hat ja jemand eine Idee wie ich halt den Innenwinkel von 30 Grad zeigen ohne die Trigonometrie zu verwenden.

Answer 4

Ich denke, die bisherigen Antworten sollten um ein paar Abbildungen ergänzt werden. Das erleichtert das Verständnis ungemein. Im folgenden meine Lösungsversion mit Abbildungen:

 

Wir bestimmen Fläche A, indem wir von der halben Quadratsfläche die Teilflächen (schwarz-graues Dreieck und gelben Kreissektor) abziehen:

A = Q/2 - D - K_Sektor

A = a²/2  -  1/2·h·a/2 - a²·π·30°/360°

A = a²/2 - h*a/4   - a²*π*1/12

A = a²/2 - h*a/4   - a²*π*1/12

Höhe h bestimmen:

(a/2)² + h² = a²

h² = a² - (a/2)²

h = √( a² - (a/2)² )

A = a²/2 - h*a/4   - a²*π*1/12

A = a²/2 - √( a² - (a/2)² )*a/4   - a²*π*1/12

Eine kleine Teilfläche A ergibt sich also aus dieser Gleichung. Wir haben die Teilfläche A insgesamt 8 mal. Um die gesamte farbige Fläche zu erhalten, ziehen wir von dem Quadrat a² die 8*A ab:

A_farbig = A_Quadrat - 8*A_Teil 

A_farbig = a²        - 8 * (a²/2 - √( a² - (a/2)² )*a/4   - a²*π*1/12)

Sei a = 2, so erhalten wir:

A_farbig = a²  - 8 * (a²/2 - √( a² - (a/2)² )*a/4   - a²*π*1/12)

A_farbig = 2²  - 8 * (2²/2 - √( 2² - (2/2)² )*2/4   - 2²*π*1/12)

A_farbig = 4  - 8 * (4/2 - √( 4 - (1)² )*1/2   - 4*π*1/12)

A_farbig = 4  - 8 * (2 - √( 3 )*1/2   - π*1/3)

A_farbig ≈ 3,306 Flächeneinheiten