Question

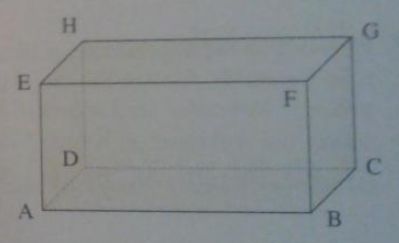
Prüfen Sie anhand des abgebildeten Quaders, ob die gegebenen drei Vektoren komplanar sind.

a) \( \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{AE}}, \overrightarrow{\mathrm{AF}} \)

b) \( \overrightarrow{\mathrm{AB}}, \overrightarrow{\mathrm{CG}}, \overrightarrow{\mathrm{EA}} \)

c) \( \overrightarrow{\mathrm{AE}}, \overrightarrow{\mathrm{DC}}, \overrightarrow{\mathrm{FG}} \)

d) \( \overrightarrow{\mathrm{HE}}, \overrightarrow{\mathrm{BC}}, \overrightarrow{\mathrm{AG}} \)

e) \( \overrightarrow{\mathrm{AC}}, \overrightarrow{\mathrm{FG}}, \overrightarrow{\mathrm{HD}} \)

Ansatz:

(b) komplanar

(d) komplanar

Ich dachte bisher, komplanare Vektoren befänden sich in einer Ebene. Das sind die Vektoren in (b) und (d) doch gar nicht! Oder gibt es noch eine andere Form von Komplanarität, die ich nicht kenne?

Answer 1

bei b) ist doch AE und CG der gleiche Vektor. Dazu müssen die sich nicht am selben Ort befinden. Es langt wenn sie in die gleiche Richtung weisen und gleich lang sind.

bei d) ist HE = -BC.

Wenn von 3 Vektoren bereits 2 linear abhängig sind ist der dritte Vektor egal. Sie sind dann in jedem Fall linear abhängig.

Comments

Ja, aber ich habe gedacht die müssen dann alle 3 in einer Ebene liegen, damit sie komplanar sind. Wenn 2 Vektoren in einer Ebene liegen und linear abhängig ist. Dann kann ich einen beliebigen Vektor dazunehmen und der ist auch komplanar, obwohl er nicht in der Ebene ist?! :O

---

Komplanare Vektoren müssen zur gleichen Ebene parallel verlaufen. Vektoren haben nur eine Richtung und eine Länge aber keine Lage im Raum.

---

Holy shit! Ich habe mir immer vorgestellt, dass die in einer Ebene liegen müssen. Darum habe ich gedacht, dass bei (b) der Vektor CG nicht in derselben Ebene liegt wie AB und EA und das daher die Vektoren nicht komplanar sind. Weil man also CG durch Parallelverschiebung in die Ebene von AB und EA überführen kann, sind die Vektoren also komplanar. Aha. Da soll mal einer drauf kommen.  Auch an Mathecoach. Ich würde dir gern den Beste-Antwort-Stern geben aber meine Cookies von sind weg, das geht also nicht mehr. LG

---

Man muss sich alle Vektoren ausgehend von einem Punkt vorstellen. Also du legst alle Vektoren an einen Ausgangspunkt. Und wenn sie dann in einer Ebene liegen sind sie komplanar.

---

Und wenn das der Fall ist, dann liegen sie auch alle auf einer Geraden - tadaaaaaaaa !!! :-)

---

Nein. Wie kommst du jetzt da drauf ?

AB und AE liegen in einer Ebene.
HD und GC oder auch BF würden jetzt auch in der Ebene liegen.