Hallo,
Voraussetzung für die Entdeckung des Satzes über die Winkelsumme im n-Eck sollte sein, dass die Winkelsumme im Dreieck bekannt ist.
1.) Man nehme ein konkretes n-Eck (z.B. ein Fünfeck) und zerlege (zerschneide) es ausgehend von einer Ecke (hier \(C\)) in \(n-2\) Dreiecke. Jetzt kann man die Winkel noch bunt anmalen - in jedem Dreieck eine andere Farbe - und dann das Dreieck wieder zum n-Eck zusammen setzen.
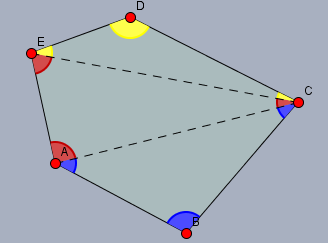
Wie groß ist nun die Summe aller Winkel?
2.) es existiert ein beliebiges n-Eck. Nun füge einen neue Ecke ein, indem einfach ein Punkt \(P\) auf einer Seite zur Ecke erklärt wird.
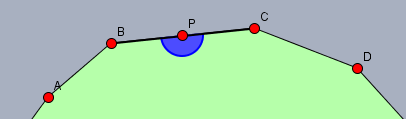
Wie groß ist nun die Anzahl der Ecken verglichen mit vorher? Und wie hat sich die Winkelsumme der Figur geändert?
3.) Ist die Winkelsumme nur von der Anzahl der Ecken abhängig? Was passiert mit den Winkeln in der Umgebung eines Eckpunktes \(Q\) eines n-Ecks, wenn man die Position von \(Q\) verändert?
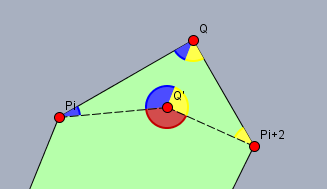
Betrachte eine Ecke \(Q\) zwischen den Ecken \(P_i\) und \(P_{i+2}\). Nun verschiebe den Punkt \(Q\) in die Position \(Q'\). Was passiert dabei mit der Winkelsumme in diesem n-Eck?
Tipp: die Winkelsumme in dem Viereck \(P_iQ'P_{i+2}Q\) beträgt \(2\cdot 180° = 360°\). Die Winkelsumme um den Punkt \(Q'\) herum beträgt ebenso \(360°\) (blauer, gelber und Winkel um \(Q'\)). Was kann man daraus folgern?