Optimierungsaufgabe quadratische Funktionen

Question

Aufgabe:  Meine Aufgabe lautet

Ein 18 cm langer Draht soll zu einem Rechteck gebogen werden.

a) Für welche Seitenlänge x ist der
  Flächeninhalt am größten?
b) Wie groß ist dieser Flächeninhalt?

Wir hatten das Thema in der Schule besprochen aber ich war nicht anwesend also bitte mit Rechenschritte erklären.

Danke schon voraus:)

Problem/Ansatz: Mein Lehrer hatte schon auf der Tafel ein Rechteck gezeichnet oben und unten stand x und links und rechts stand \(\frac{18-2x}{2}\)

Answer 1

Eine Seite ist a = x und die andere b = (18 - 2x)/2 = 9 - x

a)

Fläche

A = x*(9 - x) = 9x - x^2

A' = 9 - 2x = 0 → x = 4.5 cm

b)

a = 4.5

b = 9 - 4.5 = 4.5

A = 4.5^2 = 20.25 cm²

Comments

Vielen Dank aber was ist a) und was ist b) ?

---

Ich habe dir das deutlich dazu geschrieben.

Answer 2

Im Grunde ist das nur eine Kurvendiskussionsaufgabe verpackt in einem Optimierungsproblem.

Ich habe mal das Rechteck so aufgezeichnet:

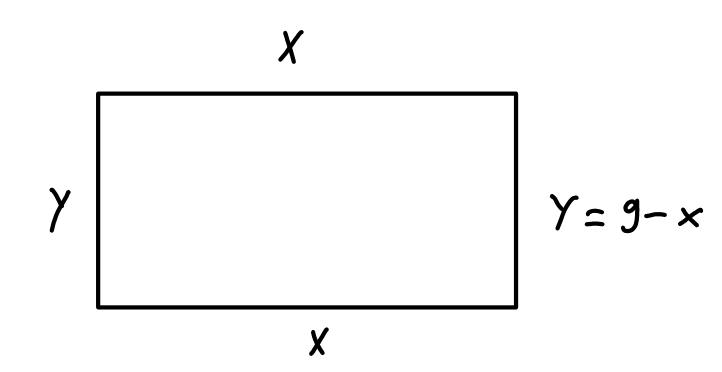
Es geht darum, die Fläche zu beschreiben. Bei einem Rechteck ist das erstmal \(A(x,y)=x\cdot y\), deine sogenannte Hauptbedingung. Jetzt hast du noch die Information, 18cm langes Draht zu haben, was einen Einfluss auf die Optimierung haben wird. Der Umfang lässt sich damit als Nebenbedingung dieses Problems so beschreiben \(18=U(x,y)=x+y+x+y=2\cdot (x+y) \).

Jetzt stellt man eine sogenannte Zielfunktion auf, die deine Fläche unter Berücksichtung des Umfanges (18cm) beschreibt. Da kommt die Nebenbedingung ins Spiel. Löse diese nach einer Unbekannten auf, zb nach y:  y=9-x. Das setzt man in die Hauptbedingung ein:

\(A(x)=x\cdot (9-x)\), deine Zielfunktion. Diese Flächeninhaltsfunktion soll nun maximiert werden. Führe nun dazu eine Kurvendiskussion durch.