Hallo,
Teile die Halbkugel in Z-Richtung in Ringe auf, die die Oberfläche \(\text dA\) haben. Dann gilt für den Z-Koordinate \(\overline z\) des Schwerpunkts der Oberfläche der Halbkugel mit Radius \(R=1\) und Fläche \(A\):$$ A \cdot \overline z = \int_0^1 z \, \text dA$$Das \(A\) für die Halbkugel ist hier \(A=|S|=2\pi\) (siehe Wiki), aber dies darst Du ja nicht benutzen. Spielt aber keine Rolle, da das \(A\) schlicht die Summe aller \(\text dA\) ist - also gilt:$$\overline z = \frac 1A \int_0^1 z \, \text dA = \frac { \int_0^1 z \, \text dA}{ \int_0^1 1 \, \text dA}$$
Die erste Frage ist: was ist \(\text dA\)? Setze dazu zunächst \(x^2+y^2=r^2\); daraus folgt dann auch aus \(x^2+y^2+z^2=1\) gleich$$r= \sqrt{1-z^2}$$und dann sieht man sich das mal genau an:
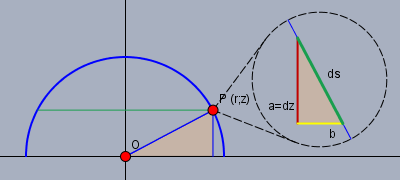
Hier siehst Du einen Schnitt durch die Halbkugel (blau). Der Punkt \(P\) hat im Bild die Koordinaten \(P=(r;z)\). Die grüne waagerechte Strecke ist die Projektion eines der oben erwähnten Ringe mit der Fläche \(\text dA\). Der Ring hat den Durchmesser \(r\). Der schwarze Kreis rechts daneben ist die Lupe, mit der ich \(P\) betrachte. Die schräge grüne Strecke sei \(\text ds\). Daraus folgt schon:$$\text dA = 2\pi r \, \text ds $$Die senkrechte rote Strecke in der Lupe sei \(a\) und die waagerechte gelbe sei \(b\). Weiter sind die beiden markierten Dreiecke ähnlich. Aus all dem folgt:$$\begin{aligned}\frac ba &= \frac {z}r \\ b &= \frac {z}r a \\ \text ds &= \sqrt{a^2 + b^2} = \sqrt{a^2 + \left( \frac {z}r a\right)^2} \\&= a\sqrt{1 + \left( \frac {z}{\sqrt{1-z^2}} \right)^2} = a \sqrt{\frac{1 - z^2 + z^2}{1- z^2}} \\&= \frac a {\sqrt{1-z^2}}\end{aligned}$$Nun ist aber das \(a\) - also der senkrechte Ausschnitt - das \(\text dz\). Dies bedeutet für \(\text dA\)$$\begin{aligned}\text dA &= 2\pi r \, \text ds \\&= 2 \pi \sqrt{1-z^2} \cdot \frac {\text dz} {\sqrt{1-z^2}} \\&= 2\pi \, \text dz\end{aligned}$$D.h. das \(\text dA\) ist nicht mehr von \(z\) abhängig. Mit etwas Erfahrung in der Berechnung von Schwerpunkten kann man jetzt schon sagen, dass daher \(\overline z = R/2 = 1/2\) sein muss. Aber lass uns das formal bestätigen:$$\begin{aligned} \overline z &= \frac { \int_0^1 z \, \text dA}{ \int_0^1 1 \, \text dA} = \frac {\pi \int_0^1 2z \, \text dz}{2\pi \int_0^1 1 \text dz} \\&= \frac 12 \cdot \frac {\left. z^2 \right|_0^1}{\left. z \right|_0^1} = \frac 12 \cdot \frac 11 \\&= \frac 12\end{aligned}$$Falls noch Fragen offen sind, so melde Dich bitte.