Die Kosten für die Herstellung von Stühlen setzen sich aus Fixkosten von 25.000 € und variablen Kosten von 35 € für jeden einzelnen Stuhl zusammen. Ein Stuhl wird für 95 € verkauft.
a) Geben Sie den Gewinn (Einkommen minus Kosten) in Abhängigkeit von der Anzahl x der Stühle an.
K(x) = 35x + 25000
E(x) = 95x
G(x) = E(x) - K(x) = 95x - (35x + 25000) = 60x - 25000
b) Zeichnen Sie die Gewinnfunktion. Berechnen Sie den Gewinn für 5000 Stühle.
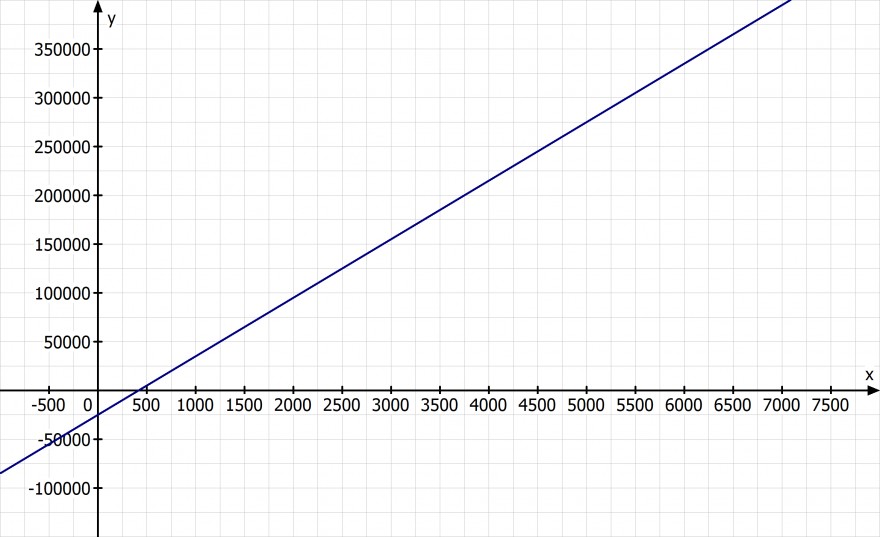
G(5000) = 275000 €
c) Bestimmen Sie die Anzahl der Stühle, mit denen das Unternehmen Gewinne erzielt.
G(x) > 0 --> x ≥ 417 Stühle