Verkettung von Beträgen

Question

Aufgabe:

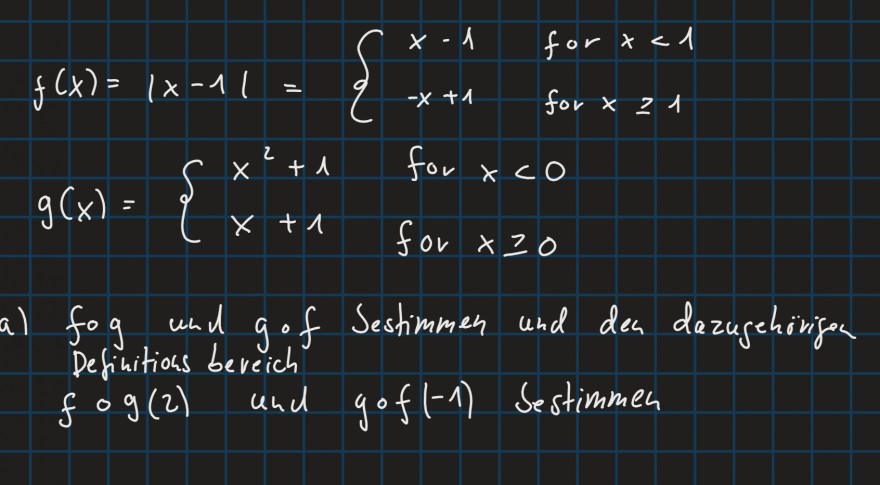
Text erkannt:

\( f(x)=|x-1|=\left\{\begin{array}{cl}x-1 & \text { for } x<1 \\ -x+1 & \text { for } x \geq 1\end{array}\right. \)
\( g(x)=\left\{\begin{array}{ll}x^{2}+1 & \text { for } x<0 \\ x+1 & \text { for } x \geq 0\end{array}\right. \)
a) fog und gof bestimmen und den dazugehörigen Definitionbereich ermitteln

\( f \circ g(2) \) und \( g \circ f(-1) \) bestimmen

Problem/Ansatz:

Ich habe ein Problem mit Beträgen , verstehe nicht wie man diese mit ihren Fällen richtig bearbeitet

Ich weiß das f*g dann |x^2| und |x| ist aber ich verstehe nicht wie ich die Intervalle wählen muss dafür.

Kann jemand mir  helfen?

Answer 1

Ich habe ein Problem mit Beträgen , verstehe nicht wie man diese mit ihren Fällen richtig bearbeitet

Die Beträge interessieren doch nicht mehr - hinter der geschweiften Klammer ist doch bereits angegeben, wie man diese für x>1 und für x≤1 ohne Betragsstriche interpretieren kann.

Du musst also nur noch diese Fallunterscheidung machen, wobei wegen der zweiten Funktion g(x) im Fall x<1 nochmal zwischen den beiden Unterfällen x<0 und 0≤x<1 unterschieden werden muss.