f(x)=a*x^3+b*x
f(3)=a*3^3+b*3
27a+3b=3
9a+b=1
b=1-9a
f(x)=a*x^3+(1-9a)*x
f´(x)=3*a*x^2+1-9a
3*a*x^2=9a-1
f´´(x)=6*a*x
6*a*x=0
Wendepunkte bei x=0 und y=0
waagerechte Wendetangente:
f´(0)=1-9a
1-9a=0
a=\( \frac{1}{9} \)
f(x)=\( \frac{1}{9} \)*x^3 rot in der Zeichnung
Alle anderen Funktionen außer a=0 ->Gerade durch A(3|3) haben ein lokales Maximum und somit auch ein lokales Minimum.
mfG
Moliets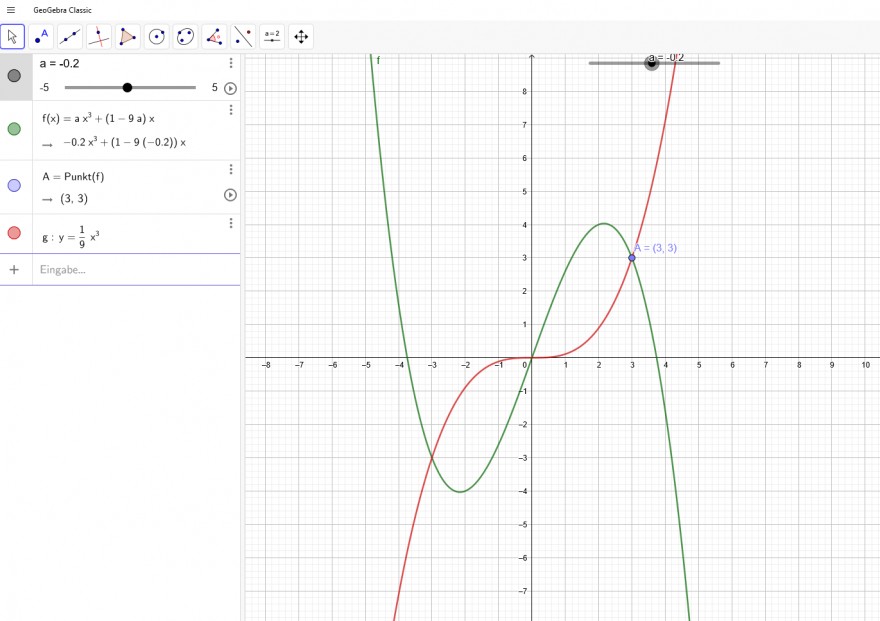
Text erkannt:
\( a=-0.2 \)
0
5
\( f(x)=a x^{3}+(1-9 a) x \)
O \( --0.2 x^{3}+(1-9(-0.2)) \times \)
O \( A= \) Punkt \( (f) \)
\( -(3,3) \)
g: \( y=\frac{1}{9} x^{3} \)
Eingabe.
mfG
Moliets