Aufgabe:
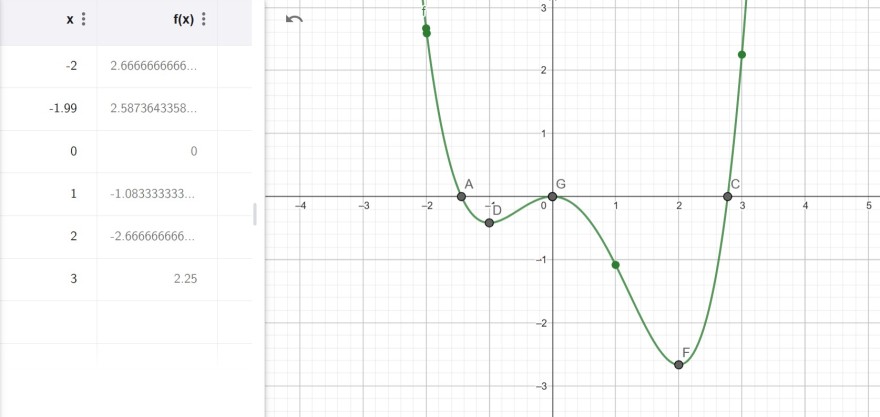
Gegeben ist im Intervall I =(-2; 3] die Funktion f(x) = (1/4)x^4-(1/3)x^3-x^2
Geben Sie alle gloablen Maxima und Minima an.
Problem/Ansatz:
Es gibt zwei lokale Minima:f(-1)=-5/12 und f(2)=-8/3
Und ein lokales Maximum: f(0)=0
f besitzt damit das globale Minimum -8/3
Am rechten Rand hat die Funktion das Randmaximum f(3)=9/4 und am linken Rand existiert kein Randmaximum, da -2 nicht zur Defintionsmenge gehört. f(3)=9/4 ist kein globales Maximum, da in der Umgebung von x=-2 Funktionswerte existieren, die größer sind als f(3)=9/4. Wieso kann ich allerdings nicht x=-1,99 als Randmaximum angeben, denn f(-1,99)= 2,59 > f(3)=2,25 ?