Sekante zwischen Hoch- und Tiefpunkt

Question

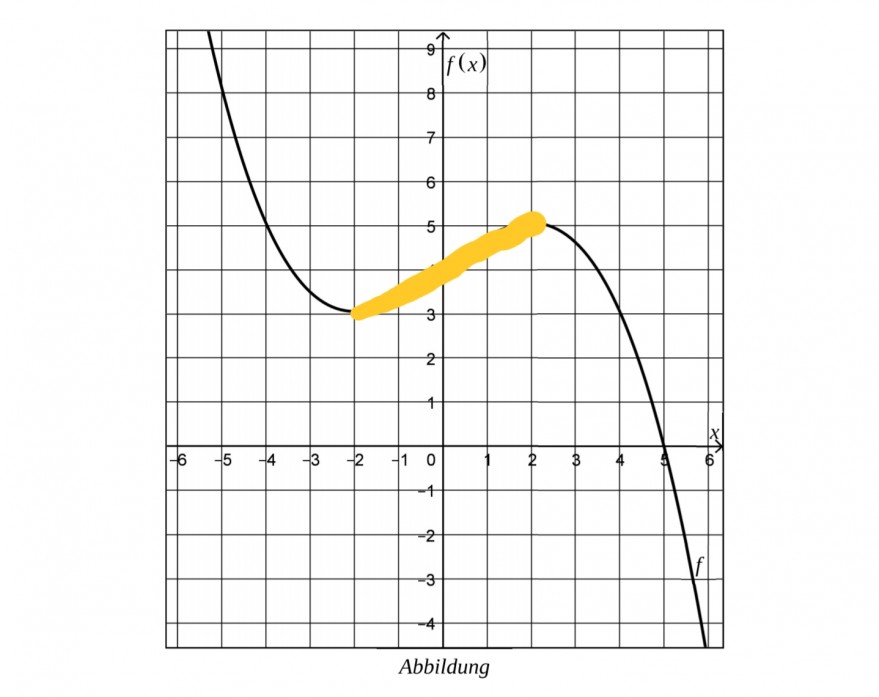
Aufgabe:

Gegeben ist die Funktion \( f \) mit der Gleichung
\( f(x)=-\frac{1}{16} \cdot x^{3}+\frac{3}{4} \cdot x+\frac{65}{16}, x \in \mathbb{R} \)

c) Die Sekante \( s \) verläuft durch den Tiefpunkt \( T\left(-2 \mid \frac{49}{16}\right) \) und den Hochpunkt \( H\left(2 \mid \frac{81}{16}\right) \)
des Graphen von \( f \).
(1) Zeichnen Sie die Sekante s in die Abbildung ein und bestimmen Sie rechnerisch die
Steigung von s.

Problem/Ansatz:

So sieht der Graph aus:

Ist meine Sekante so richtig eingezeichnet? ( Angenommen die Linie ist dünner), Steigung kann ich selbst berechnen, bin mir aber bei der Zeichnung nicht sicher haha :

Answer 1

Meine Skizze sieht wie folgt aus

~plot~ -1/16*x^3+3/4*x+65/16;1/2*x+65/16;[[-8|8|-2|10]] ~plot~