Zwei geradelinig verlaufende

Question

Aufgabe: Zwei geradlinig verlaufende Eisenbahntrassen, die in den Punkten A und B enden, sollen miteinander verbunden werden. (s. Abbildung.)Bestimmen Sie rechnerisch die Gleichung einer zum Ursprung punktsymmetrischen Funktion dritten Grades einer Verbindungskurve, die in A und B ohne Knick an die Trassen anschließt.

Problem/Ansatz:

Da soll rauskommen -0,023x³+1,125x Bei mir wenn ich das in lineare Gelcihungssystem EIngabe kommt Null raus danke für jede hilfe

Ich rechne

f(x)ax³+bx f'(x)=3ax²+b   Ist ja eine Punktsymmetrische Funktion 3 Grades

f(4)=64a+4b=3 → Punkt B

f(0)=a+b=0     --->Punkt =0/0

f(-4)=-64a-4b=-3 ---->Punkt A

f'(-4)=-48a+b=-3 → Bei Punkt A ist ja ein Knick deswegen f'

Text erkannt:

$\equiv$ GeoGebra Rechner Suite
$x$
$\mathbf{I}$

Answer 1

Ist doch ein guter Ansatz. Du brauchst nur

f(4)=3   und f ' (4)=0  [ Die Trasse läuft ja waagerecht weiter ! ]

Mit deinem Ansatz  f(x) = ax³+bx   f'(x)=3ax²+b folgt

64a + 4b = 3     und  48a + b = 0 
                                ==>   a = -b/48

-(4/3)b + 4b = 3
 ==> b=9/8 =1,125          und   a =-3/128 =-0,023438

Comments

Also ist es dann so richtig ?

f(4)=-64a+4b=-3 → A

f'(4)=48a+b=0 ------>A mit knick

f(4)=64a+4b=3------>B

f(0)=a+b=0 Ursprung

Wenn ich das in meinen Taschenrechner eingebe kommt da nichts raus

---

Zudem müsste es nicht auch so sein das F' nicht -4 ist ?

Danke für die Antwort

Answer 2

Die Ableitungen bei 4 und -4 sollen sicher nicht -3, sondern 0 sein.

Comments

Wie meinst du kannst du das mal aufschreiben ?

---

Gehts noch? Du wirst wohl noch selbst in deinen beiden falschen Ableitungsgleichungen statt der -3 eine 0 hinschreiben können.

Answer 3

Gehe aus von der Parabel

u(x):=a x³+b x² + c x

{u(-4)=-3,u(4)=3, u'(4)=0} Edit

$\small \left\{ -64 \; a + 16 \; b - 4 \; c = -3, 64 \; a + 16 \; b + 4 \; c = 3, 48 \; a + 8 \; b + c = 0 \right\}$

dieses LGS kannst Du im CAS auflösen

oder ersetze a=x, b=y, c=z

$Solve \small (\{-64 x+16 y-4 z=-3,64 x+16 y+4 z=3,48 x+8 y+z=0\})$
$\rightarrow\left\{\left\{x=\frac{-3}{128}, y=0, z=\frac{9}{8}\right\}\right\}$

oder ein einem Rutsch

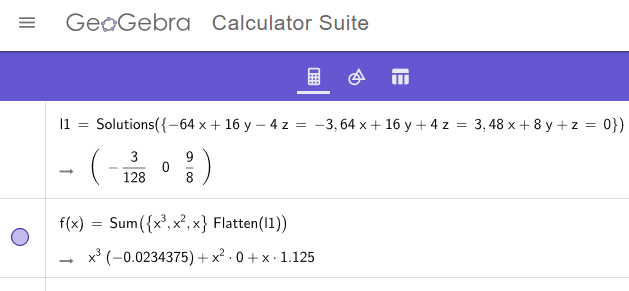
Edit: Ableitung korrigert