Hallo,
.. ein bißchen eine schwere Geburt ;-)
aus den vielen Kommentaren und aus Georgs Skizze kann man auf folgendes schließen:
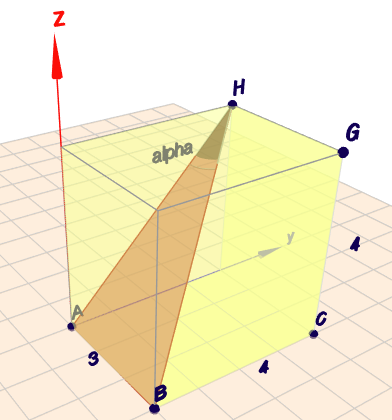
(klick auf das Bild)
Für den Winkel \(\alpha\) gilt dann:$$\tan( \alpha) = \frac{|AB|}{|AH|} = \frac{3}{\sqrt{4^2 + 4^2}} = \frac 38 \sqrt 2 \\ \implies \alpha = \arctan\left( \frac 38 \sqrt 2\right) \approx 27,94°$$Gruß Werner