Hallo,
mache zunächst eine Skizze:
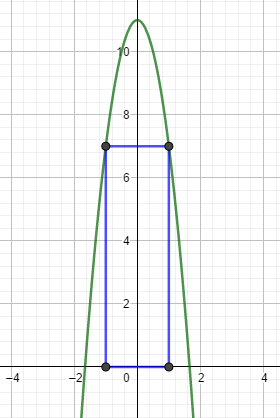
Du siehst dann, dass der Flächeninhalt A des Rechtecks sich ergibt aus 2x (Strecke zwischen den Nullstellen) und f(x).
Multipliziere also 2x mit f(x) = -4x^2 + 11, bilde die 1. Ableitung, setze sie gleich null und löse nach x auf. Setze dein Ergebnis in die Ausgangsgleichung ein, um die Seitenlänge f(x) zu bestimmen.
Gruß, Silvia