Hallo proluci,
Ich verstehe es einfach nicht.
mag ja sein, aber wenn Du es verstehen möchtest, dann könnten wir Dir besser helfen, wenn Du konkrete Fragen stellst. oder was meinst Du?
Eine Skizze hast Du ja gemacht - das ist sehr gut. Hast Du den Winkel β auch vermessen? Da sollten so 110° raus kommen. Und das kann man sich so überlegen:
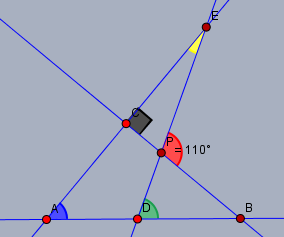
Der gelbe Winkel bei E sei φ. Dann folgt aus der Winkelsumme im Dreieck △ADEα1+(180°−α2)+φ=180°⟹φ=α2−α1=20°Und aus der Winkelsumme im Dreieck △CPE folgt90°+γ+(180°−β)=180°β=90°+γ=90°+α2−α1=110°