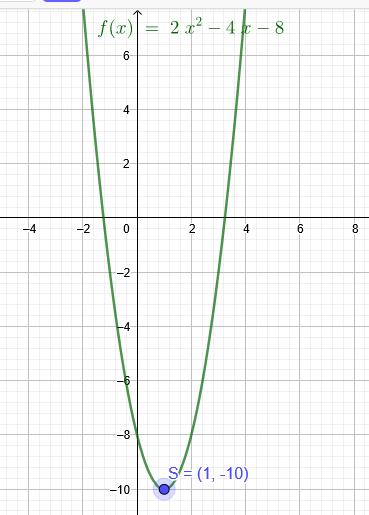
Scheitelpunkt von f(x)=2x2-4x-8 , Quadratische Ergänzung?

Question

Aufgabe:

Scheitelpunkt von $$f(x)=2x^{2}-4x-8$$, Quadratische Ergänzung?

Problem/Ansatz:

Der Lösungsweg an sich ist online auf youtube unter

nachvollziehbar. Es führen manchmal mehr als nur ein Weg nach oben, so habe ich in meinem Tabellenbuch die Formel für einen Scheitelpunkt des Graphen in der Form $$S(-\frac{b}{2a}/\frac{4ac-b^{2}}{4a} )$$gefunden und entsprechend die parameter der quadratischen funktion von oben eingesetzt und bin leider nicht auf das richtige ergebnis gekommen. woran liegt das, bzw. wozu gibt es dann diese Formel, wenn man sowieso mit der quadratischen Ergänzung arbeiten muss?

lg

Comments

Die Formel ist richtig. Wie jede Formel kürzt sie einen ggf. längeren Rechenweg, hier etwa über die quadratische Ergänzung, ab.

---

ok, mein Fehler, war zu blöd zum einsetzen

Answer 1

Ich mache es so:

y=2x²- 4x - 8 |:3

y/2=x² - 4x - 4  |+5

y/2+5=x² - 4x +1   | bin. Formel

y/2+5=(x-1)²  |·2

y+10=2·(x-1)²  |-10

y=2·(x-1)² - 10

Scheitel (1|-10)

Comments

vielen Dank für deine Antwort, ich würde es auch genau so machen, nur meine Frage sollte mehr oder weniger heissen, warum das im Mathematikunterricht so komplex mit quadratischer ergänzung reingepaukt wird, wenn man die Parameter der allgemeinen Form einfach in $$(S(-\frac{b}{2a}/\frac{4ac-b^{2}}{4a} )$$ einsetzen kann und auch so drauf kommt.

also hat das irgendwelche nachteile, die mir daraus entstehen, wenn ich das allgemein immer so mache über die "Koordinatenform"?

---

Der Nachteil ist ein Mehraufwand an Rechnung. Das Einsetzen in eine fertige Formel geht natürlich schneller. Ich kann mir diese Formel aber nicht merken und muss sie erst in der Formelsammlung suchen. Da bin ich auf meinem Wege dann doch schneller.

Answer 2

Scheitelpunktbestimmung:

y=2x²-4x-8|:2

$\frac{y}{2}$ =x^2-2x-4|+4

$\frac{y}{2}$+4 =x^2-2x|+quadratische Ergänzung(-$\frac{2}{2}$)^2=1

$\frac{y}{2}$+5 =x^2-2x+1

$\frac{y}{2}$+5 =(x-1)^2|-5

$\frac{y}{2}$ =(x-1)^2-5|*2

y=2*(x-1)²-10

S(1|-10)

Schnellerer Weg über Ableitung:

y=2x²-4x-8

y´=4x-4

4x-4=0

x=1      y(1)=2*1²-4*1-8=-10        S(1|-10)

Answer 3

f(x) = 2·x² - 4·x - 8

Scheitelpunkt

Sx = -b / (2·a) = -(-4) / (2·(2)) = 4/4 = 1

Sy = f(1) = 2·(1)² - 4·(1) - 8 = -10

Scheitelpunkt ist daher S(1 | -10)