Hallo,
es wird ja allen Anschein nach über ein Gebiet integriert, das so aussieht
~plot~ ln(x);x=1;x=e;[[-0.5|3.7|-1|2]] ~plot~
Das Gebiet ist nach 'oben' durch die Funktion \(y=\ln(x)\) bzw. \(x=e^y\) (blau) begrenzt, nach 'rechts' durch \(x=e\) und nach 'unten' durch \(y=0\). Die Funktion ist \(f(x,y) = y\); aber das ist hier nicht so wichtig.
Wenn man mit der Integration in Y-Richtung beginnt, so denke Dir eine Gerade, die in Y-Richtung verläuft, und die verläuft von unten \(x=0\) bis zur blauen Kurve \(y=\ln(x)\). Also$$\dots = \int_0^{\ln(x)} y\,\text dy = \frac12\ln^2(x)$$das kann man sich vorstellen, wie die Fläche eines Dreieckes, welches senkrecht auf der Ebene steht und die Grundseite läuft von \(0\) bis \(\ln(x)\). Je nachdem an welcher Stelle \(x\) das Dreieck steht, ist es unterschiedlich groß.
Und das folgende Integral addiert alle diese Dreiecksfläche mal \(\text dx\) zu einem Volumen.
Beginnt man mit der Integration in X-Richtung, so steht dort zwangsläufig $$\dots = \int_{x=e^y}^{x=e} y\,\text dy = \left[y\cdot x\right]_{e^y}^e = y\cdot e - y\cdot e^y$$d.h. diese besagte Fläche ist nun ein Rechteck. Ein Rechteck deshalb, da sich seine Höhe \(y\) bei einem konstanten \(y\) nicht ändert. Dieses Rechteck steht zwar senkrecht zur Ebene, aber liegt horizontal oben im Bild. Und seine Kante, mit der es auf der Ebene steht, verläuft von der blauen Kurve \(x=e^y\) bis zur grünen Senkrechten \(x=e\).
Nachtrag:
die Integrationsreihenfolge - insbesondere bei so einem Volumenintegral - gibt nur an, welche 'Scheiben' zuerst berechnet werden. Beginnt man mit der Integration über \(y\), dann wird zuerst in Y-Richtung geschnitten ...
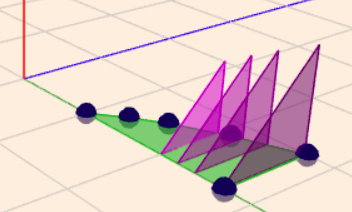
... so wie oben zu sehen. Über dem grünen Gebiet wird das 'Volumen' darüber in Scheiben geschnitten, die parallel zur YZ-Ebene stehen. DIe innere Integration berechnet die Fläche der Scheiben in Abhängigkeit von \(x\). Die äußere Integration gibt ihnen die Dicke \(\text dx\) und zählt die Scheiben zum Volumen zusammen.
Beginnt man mit der Integration über \(x\) ....
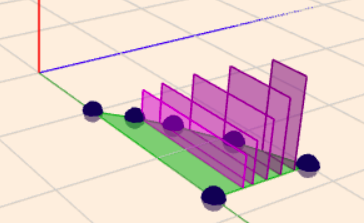
.... so stehen die Scheiben parallel zur XZ-Ebene. In diesem Fall ist das immer ein Rechteck der 'Höhe' \(y\), aber die Länge des Rechtecks ist von \(y\) abhängig und beträgt hier \(e-e^y\). Die äußere Integration über \(y\) gibt den Scheiben dann die Dicke \(\text dy\) und addiert sie von \(y=0\) bis zur letzten Scheibe bei \(y=1\).
Wichtig: zunächst muss das Gebiet, über dem integriert wird, bekannt sein. Und erst im zweiten Schritt legt man in Abhängigkeit des Gebiets und der Funktion \(f\) die erste und zweite Integrationsrichtung fest. Und dabei fallen dann automatisch die Grenzen ab.
Frag' ruhig nach, wenn noch was unklar ist.
Gruß Werner
PS.: die Bilder oben sind wie immer zum Anklicken. Dahinter steckt dann Geoknecht3D, womit man sich das alles quasi wie in 3D betrachten kann.