Aussagen zu Rotation und Divergenz von Skalarfeld und Vektorfeld

Question

Aufgabe:

a) Sei \( M \subseteq \mathbb{R}^{3} \) offen, \( f: M \rightarrow \mathbb{R} \) ein zweimal stetig differenzierbares Skalarfeld und \( \vec{v}: M \rightarrow \mathbb{R}^{3} \) ein zweimal stetig differenzierbares Vektorfeld.
Zeigen Sie die folgenden Aussagen:
i) \( \operatorname{rot}(\nabla f)=\nabla \times(\nabla f)=\overrightarrow{0} \)
ii) \( \operatorname{div}(\operatorname{rot} \vec{v})=\nabla \cdot(\nabla \times \vec{v})=0 \)
iii) \( \operatorname{rot}(f \vec{v})=(\nabla f) \times \vec{v}+f \operatorname{rot} \vec{v} \).

b) Gesucht ist der Flächeninhalt des durch den roten Rand gekennzeichneten Kreissegments \( K_{\alpha} \) mit Radius 1, welches vom Mittelpunktswinkel \( \alpha \in(0,2 \pi) \) abhängt.

Gehen Sie zur Berechnung des gesuchten Flächeninhaltes wie folgt vor:
(1) Parametrisieren Sie die Kurve \( \gamma_{1} \) abhängig vom Winkel \( \alpha \).
(2) Parametrisieren Sie die Kurve \( \gamma_{2} \) als Strecke von \( B \) nach \( A \).

Problem/Ansatz:

Nach 2 Urlaubssemestern bin ich anscheint komplett raus aus den Themen von HöMa 2 und komme in HöMa 3 noch nicht wirklich rein. Ich verstehe schon die Aufgabenstellung (zweimal stetig differnzierbares Skalarfeld?) nicht und würde mich über Ansätze oder (ich weiß die Anfrage ist hier nicht gern gesehen) Lösungswege freuen. Ich kann mir mit Lösungswegen oft einiges wieder herleiten.

Comments

Sorry, aber das sind mir zu viele Aufgaben in einer Frage...

---

Fortsetzung

Titel: Fläche von einem Kreissegment berechnen

Stichworte: integralrechnung

Aufgabe: Fläche von einem Kreissegment.

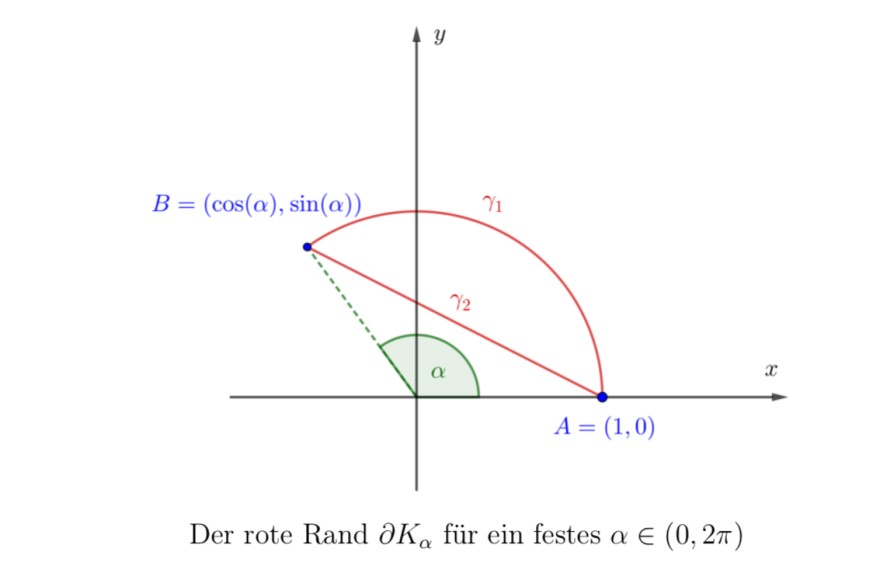
Gesucht ist der Flächeninhalt des durch den roten Rand gekennzeichneten Kreisseg-
ments Kα mit Radius 1, welches vom Mittelpunktswinkel α ∈ (0, 2π) abhängt.

Gehen Sie zur Berechnung des gesuchten Flächeninhaltes wie folgt vor:
(1) Parametrisieren Sie die Kurve γ1 abhängig vom Winkel α.

(2) Parametrisieren Sie die Kurve γ2 als Strecke von B nach A.

(3) Verwenden Sie den Satz 25.8, um den Flächeninhalt des gesuchten Kreissegmentes zu berechnen.

Text erkannt:

Der rote Rand \( \partial K_{\alpha} \) für ein festes \( \alpha \in(0,2 \pi) \)

Problem/Ansatz: Ich weiß nicht zurecht wie bei der Aufgabe rangehen soll?

---

Ganz einfach:

(1) Parametrisieren Sie die Kurve γ1 abhängig vom Winkel α.

Die Parametrisierung ist bereits in Form der Koordinaten von B gegeben!

(2) Parametrisieren Sie die Kurve γ2 als Strecke von B nach A.

Tu es. (Stichwort: Parameterform eine Geradengleichung. Dein Parameter durchläuft nur nicht alle reellen Zahlen, sondern von ... bis ...)

---

Abgesehen davon, dass Du nicht verrätst was Satz 25.8 ist, wurde die Frage vor zwei Tagen schon gestellt.

Answer 1

Hallo

du hast das Skalarfeld f(x,y,z) was nach R abbildet, also jedem Punkt des R^3 einen skalaren Wert (also eine Zahl) zuordnet Temperaturwerte in Abhängigkeit vom Ort z.B sind ein Skalarfeld.

v=v(x,y,z) ist ein Vektor, der jede Punkt des R^3 einen Vektor zuordnet. Beispiel wären Windrichtungen und Größe  in jedem Punkt

die Behauptungen rechnet man einfach nach! und damit a)

der Kreis steht da ja schon  als B parametrisiert,  wenn du beta durch t ersetzt, t=0 bis beta, das Geradenstück Mit A+t*AB , AB der Vektor  t von 0 bis 1