Oder kann man das eleganter erklären ?
Na ja ... probiere ich es mal. Das Kreuzprodukt sagt ja lediglich, dass der Sinus des Winkels \(\varphi\) zwischen den beiden Vektoren$$\sin(\varphi) = 8 \sqrt{\frac{2}{155}} \approx 0,9087$$beträgt - mehr nicht!
Dann werfe mal einen Blick auf den Einheitskreis und zeichne den Sinuswert dort ein:
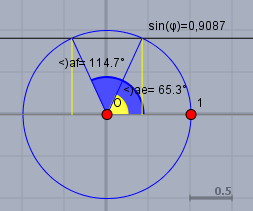
zeichnet man die Waagerechte (schwarz) bei \(\sin(\varphi) \approx 0,9087\) ein, so schneidet diese den Einheitskreis an zwei(!) Stellen. D.h. es sind zwei Winkel, für die gilt \(\sin(\varphi) \approx 0,9087\).
Das Kreuzprodukt macht also keine Aussagen darüber welcher von beiden der 'richtigere' ist!