Vom Duplikat:
Titel: Wie kommt man auf das Ergebnis der beiden Komplexen Gleichungen?
Stichworte: quadratische-gleichungen,komplexe-zahlen
Wie kommt man auf das Ergebnis der beiden Eulerschen Gleichungen? Insbesondere auf den Betrag und den Phasenwinkel... hab alles probiert, mit Wurzel ziehen etc... wie kommt man bspw auf die 105 V?
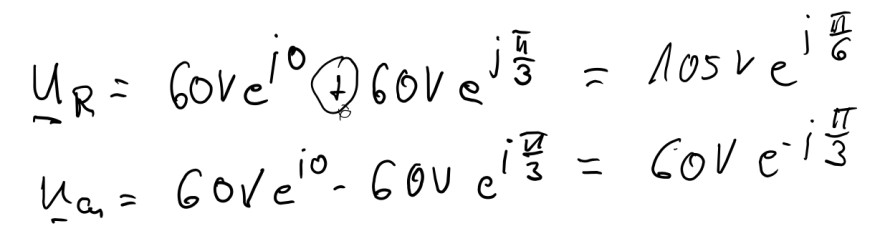
Text erkannt:
\( u_{R}=60 \mathrm{v} e^{i 0}(1) 60 \mathrm{~V} e^{j \frac{\pi}{3}}=105 v e^{j \frac{\pi}{6}} \)
\( u_{a_{1}}=60 \mathrm{~V} e^{i 0}-60 \mathrm{O} e^{i \frac{\pi}{3}}=60 \mathrm{~V} e^{-i \frac{\pi}{3}} \)