Finden Sie die Gleichung der Geraden, die durch die gegebene Punkte gehen und parallel zu den gegebenen Geraden sind (Lösungsweg dazuschreiben)
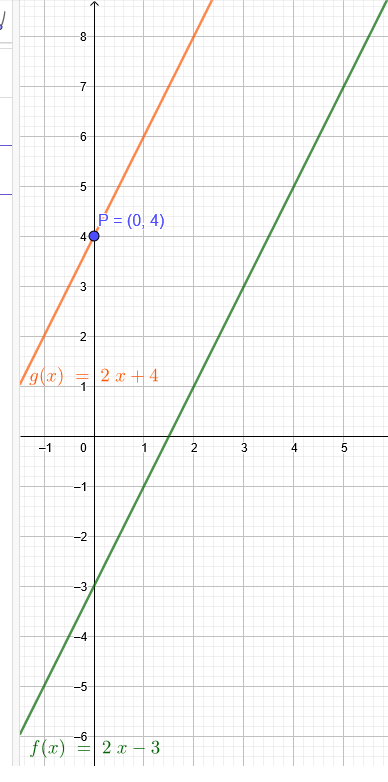
f(x)= 2x-3, P (0|4)
Die Gerade soll parallel sein. Darum hat sie auch die gleiche Steigung wie f(x)= 2x-3, m=2
Der Abschnitt auf der y-Achse ist nun nicht -3 sondern d, da unbekannt.
g(x)= 2x+d
P (0|4) liegt auf g(x)= 2x+d:
g(0)= 2*0+d
2*0+d=4
d=4
g(x)= 2x+4