Hallo,
zu a)
parallele Geraden haben die Gleichung Steigung.
Die Steigung der Geraden ist m = 3.
Setze also die 1. Ableitung = Steigung
f'(x) = 3 und löse nach x auf.
Setze deine Ergebnisse in f(x) ein, um die y-Koordinaten der Punkte zu bestimmen.
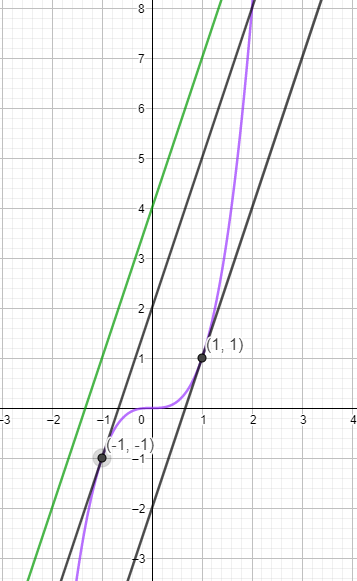
Gruß, Silvia