Hallo,
Die Koordinaten jedes Punkt, der in einer Ebene liegt, müssen die Ebenengleichung erfüllen. D.h. mit$$E:\quad 3x+y+2z=6$$liegt ein Punkt \(Q(x=1,\,y=-1,\,z=2)\) in \(E\), da die Gleichung$$3\cdot 1 + (-1) + 2\cdot 2 = 6$$aufgeht.
Soll eine Gerade \(g\) in \(E\) liegen, so muss jeder(!) Punkt der Geraden die Ebenengleichung erfüllen. Und da \((1,\,1,\,a)\) ein Punkt auf \(g\) ist, muss auch dieser die Ebenengleichung erfüllen. Daraus folgt dann der Wert für \(a\)$$\begin{aligned}3\cdot 1 + 1 + 2\cdot a &= 6 \\ 4+2a &= 6\\ 2a &= 2 \\ a&=1\end{aligned}$$Der Richtungsvektor von \(g\) soll in der Ebene \(E\) liegen und muss folglich senkrecht auf dem Normalenvektor von \(E\) stehen. Der Normalenvektor \(\vec n\) setzt sich aus den Koeffizienten der Ebenengleichung zusammen:$$E:\quad 3x+y+2z=6 \quad\Leftrightarrow\quad \begin{pmatrix} 3\\1\\ 2\end{pmatrix} \vec x = 6 \\ \vec n = \begin{pmatrix} 3\\1\\ 2\end{pmatrix}$$Stehen zwei Vektoren senkrcht auf einander, so ist ihr Skalarprodukt =0. Also gilt$$\begin{aligned}\begin{pmatrix} 3\\1\\ 2\end{pmatrix} \cdot \begin{pmatrix} b\\0\\ 3\end{pmatrix} &= 0 \\ 3b + 6 &= 0 \\ 3b &= -6 \\ b&= -2\end{aligned}$$Anbei eine Szene in Geoknecht3D, die das graphisch darstellt.
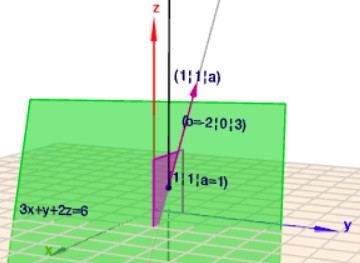
Klick auf das Bild, dann öffnet sich Geoknecht3D und Du kannst die Szene mit der Maus rotieren und bekommst einen besseren räumlichen Eindruck.
Die schwarze Senkrechte beschreibt alle Punkte, die mit \((1,\,1,\,a)\) zu erreichen sind. Folglich muss \(a\) so gewählt werden, wo diese Senkrechte die Ebene \(E\) (grün) schneidet.
Die lila Fläche beschreibt die Freiheitsgrade, die durch den Parameter \(b\) zur Verfügung stehen. Folglich ist die gesuchte Gerade die Schnittgerade von \(E\) und der lila Ebene.
Alternativ kann man auch rein anlytisch vorgehen, indem man die Geradengleichung direkt in die Ebenengleichung einsetzt. Einsetzen deshalb, weil ja gerade die Menge der Punkte gesucht ist, die in \(g\) und \(E\) liegen. Aus $$E:\space \begin{pmatrix} 3\\1\\ 2\end{pmatrix} \vec x = 6 \quad \text{und}\quad g:\space \vec x = \begin{pmatrix}1\\ 1\\ a\end{pmatrix} + r\begin{pmatrix}b\\ 0\\ 3\end{pmatrix}$$wird mit Einsetzen von \(g\) in \(E\):$$\begin{aligned}\begin{pmatrix} 3\\1\\ 2\end{pmatrix} \left(\begin{pmatrix}1\\ 1\\ a\end{pmatrix} + r\begin{pmatrix}b\\ 0\\ 3\end{pmatrix}\right) &= 6 \\ \begin{pmatrix} 3\\1\\ 2\end{pmatrix} \begin{pmatrix}1+br\\ 1\\ a+3r\end{pmatrix} &= 6\\ 3(1+br)+1+2(a+3r)&=6 \\ 3 +3br + 1 +2a + 6r &= 6 \\ 3br +2a + 6r &= 2 \\ (3b+6)r +2a &= 2\end{aligned}$$ Da jeder(!) Punkt von \(g\) in \(E\) liegen soll, muss diese Gleichung für jeden(!) Wert von \(r\) aufgehen. Das ist nur möglich, wenn der Faktor \((3b+6)\) vor \(r\) gleich \(0\) ist. Daraus folgen dann die selben Gleichungen wie oben$$3b+6=0 \implies b=-2 \\ 2a= 2 \implies a = 1$$Falls Du noch Fragen hast, so melde Dich bitte.
Gruß Werner