Zu (a)
Die Dgl. hat die allgemeine Lösung
y(t)=eAty0
Mit A=(−1188−11)=(−1100−11)+(0880)=B+C folgt
y(t)=eB+Cty0=eBeCy0 weil BC=CB gilt.
Für die Diagonalmatrix B gilt eB=(e−1100e−11) Für die antidiagonale Matrix C gilt, C2=82I
Damit gilt eC=k=0∑∞[(2k)!C2k+(2k+1)!C2k+1]=k=0∑∞[(2k)!82kI+(2k+1)!82kC]=(cosh(8)sinh(8)sinh(8)cosh(8))
Damit wird y(t)=21(e−3t−e−19te−3t+e−19t)
Zu (b)
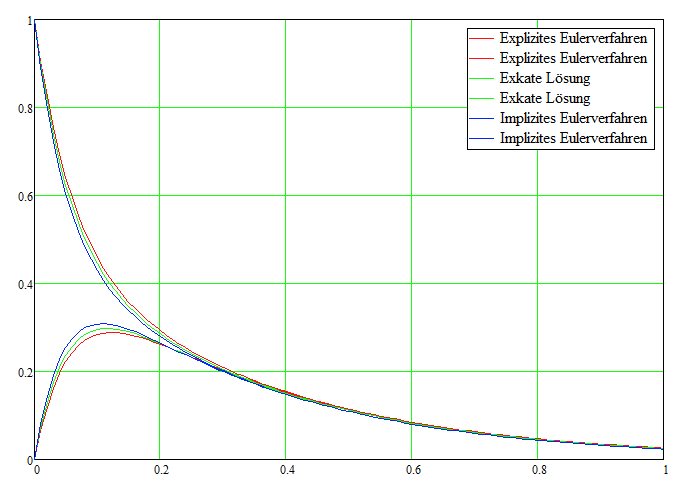
yk+1=yk+hAyk mit y0=(01)
Zu (c)
yk+1=yk+hAyk+1 mit y0=(01)
Umgestellt nach yk+1 ergibt sich
yk+1=(I−hA)−1yk
Die Lösungen sehen dann bei einer Schrittweite von h=0.01 so aus