Aufgabe:
integrieren durch Substitution
Problem/Ansatz:
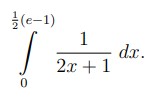
Text erkannt:
\( \int \limits_{0}^{\frac{1}{2}(e-1)} \frac{1}{2 x+1} d x \)
Ich muss diese Funktion integrieren (ohne Taschenrechner!) Ich habe versucht die Substitution anzuwenden. Dabei kam ich dann auf z=2x+1 und dx=1/2*dz. Die Neuen Grenzen habe ich gebildet in dem ich die Ursprungs Grenzen in z eingesetzt habe so bekam ich für b=e und a=1. Nun habe ich versucht die Stamfunktion von 1/z zu bilden. Dabei bekam ich dann ln(z). Die 1/2 habe ich vor dem integral gezogen. Versuche ich nun das alles auszurechnen bekomme ich 1/2* (ln(2*e+1)-ln(2*1+2). Das ergibt ca. 0.73. Allerdings ist die Lösung 0.5. Kann mir jemand erklären wo ich mich berechnet habe bzw. vielleicht einen Schritt falsch ausgeführt habe?
LG