Aufgabe:
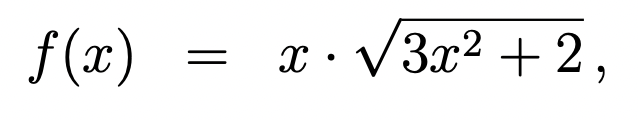
Text erkannt:
\( f(x)=x \cdot \sqrt{3 x^{2}+2} \)
Guten Tag, die Aufgabe ist es die folgende Funktion zu integrieren.
Mein Ansatz: Substitution
3x2+2 = y , also y' = 6x
Mithilfe der Physiker notation schreibe ich:
\( \frac{dy}{dx} \) = 6x => \( \frac{dy}{6x} \) = dx
Anschließend erhalte ich das neue Integral:
\( \frac{1}{6} \) * \( \int\limits_{0}^{\infty} \) x * \( \sqrt{y} \) dy (so meine ich)
Das Internet sagt mir allerdings, etwas anderes (vermutlich richtiges). Das neue Integral ist:
\( \frac{1}{6} \) * \( \int\limits_{0}^{\infty} \) \( \sqrt{y} \)
von hier aus schaffe ich es selbst, zum gewünschten Endergebnis zu kommen, allerdings stellt sich mit die Frage, wie dieses Integral zustande kommt, und was passiert mit dem x, welches sich vorher im Integral befand. Gibt es eine allgemeine Regel, wie mit dem x umzugehen ist?
Ich bedanke mich für jede Hilfe!