View Prohabilty Calculator
Ansicht Wahrscheinlichkeitsrechner
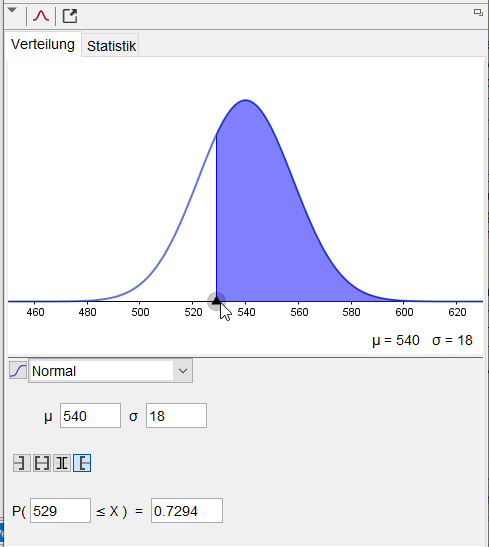
Funktionen zur Wahrscheinlichkeit
Normal( <Mittelwert>, <Standardabweichung>, <Wert der Variablen> )
InversNormal( <Mittelwert>, <Standardabweichung>, <Wahrscheinlichkeit> )
es genügt 3 Zeichen einzugeben und aus der Liste auszuwählen
je nach Version 5.x ! in der Eingabezeile/ 6.x Tripple Point auf ggb-Tastaur