Aufgabe:
Die Kantenllängen eines Quaders stehen im Verhätnis 3:5:8 zueinander.
Wie lange sind die Kanten, wenn die Körperdiagonale 1.4m misst?
Problem/Ansatz:
Ich habe die angaben l:b:h als 3x:5x:8x ersetzt und versucht nach x aufzulösen.
Leider komme ich auf das falsche Ergebnis.
Lösung: a = 0.424 m; b = 0.707 m; c = 1.131 m
Mein Ansatz:
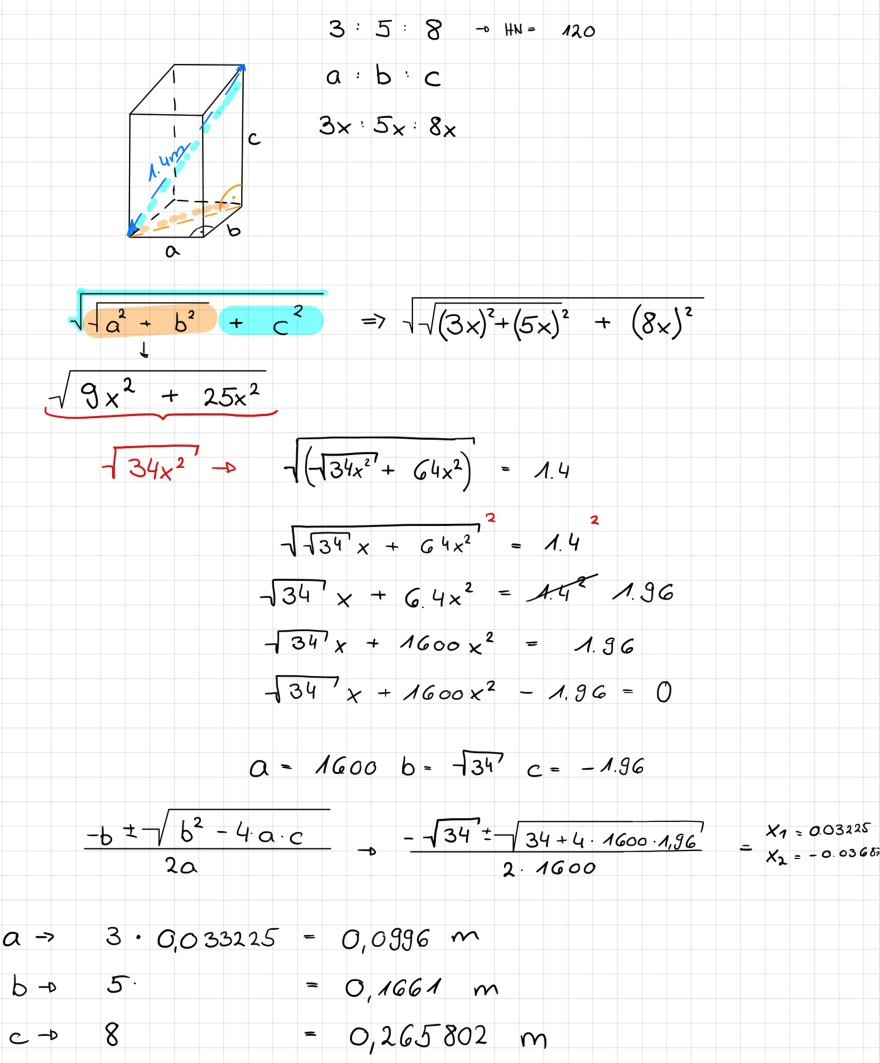
Text erkannt:
\( 3: 5: 8 \rightarrow H_{N}=120 \)
\( \sqrt{\sqrt{a^{2}+b^{2}}+c^{2}} \Rightarrow \sqrt{\sqrt{(3 x)^{2}+(5 x)^{2}}+(8 x)^{2}} \)
\( \frac{\sqrt{9 x^{2}+25 x^{2}}}{\sqrt{34 x^{2}} \rightarrow \sqrt{\left(\sqrt{34 x^{2}}+64 x^{2}\right)}}=1.4 \)
\( \sqrt{\sqrt{34} x+64 x^{2}}^{2}=1.4^{2} \)
\( \sqrt{34} x+6.4 x^{2}=4.4^{2} 1.96 \)
\( \sqrt{34} x+1600 x^{2}=1.96 \)
\( \sqrt{34} x+1600 x^{2}-1.96=0 \)
\( a=1600 b=\sqrt{34} c=-1.96 \)
\( \frac{-b \pm \sqrt{b^{2}-4 \cdot a \cdot c}}{2 a} \rightarrow \frac{-\sqrt{34} \pm \sqrt{34+4 \cdot 1600 \cdot 1,96}}{2 \cdot 1600}=\begin{array}{l}x_{1}=0.03225 \\ x_{2}=-0.0368\end{array} \rightarrow \frac{\sqrt{3 \cdot 160}}{x} \)
\( \mathrm{b}+3.033225=0,0996 \mathrm{~m} \)
\( b \rightarrow 5 .=0,1661 \mathrm{~m} \)
\( c \rightarrow 8=0,265802 \mathrm{~m} \)