Bestimmen Pyramide Kanten

Question

Aufgabe:

Problem/Ansatz: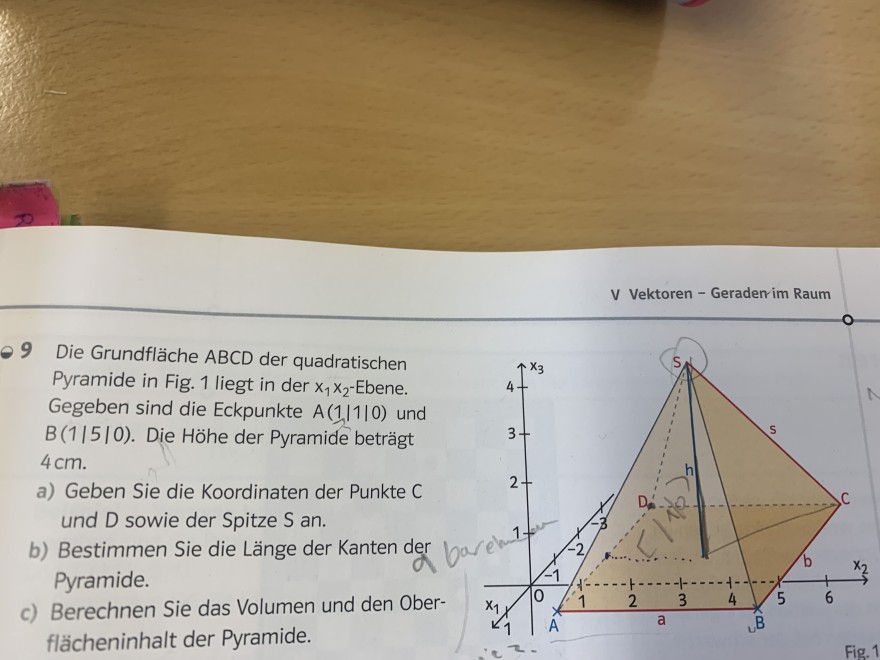

Text erkannt:

- 9 Die Grundfläche \( A B C D \) der quadratischen Pyramide in Fig. 1 liegt in der \( x_{1} x_{2} \)-Ebene. Gegeben sind die Eckpunkte \( A(1|1| 0) \) und \( B(1 / 5 / 0) \). Die Höhe der Pyramide beträgt \( 4 \mathrm{~cm} . \)
a) Geben Sie die Koordinaten der Punkte \( C \) und \( D \) sowie der Spitze \( S \) an.
b) Bestimmen Pyramide. Berechnen Sie das Volumen und den Oberc) Berechnen Sie das Volumen flächeninhalt der Pyramide.

Kann jemand mir erklären, wie man bei Aufgabe b die Kanten s, a bestimmen kann ?

Ich habe die Ergebnisse aber ich weiß nicht wie man das berechnet hat .

a= 4

s= 2 wurzel aus 6

Answer 1

a ist einfach nur die Länge von Vektor AB,

also √( (1-1)^2 +(5-1)^2 +(0-0)^2 ) = 4.

Dann mit Pythagoras s^2 = (d/2)^2 + a^2

wobei d die Diagonale des Quadrates (also a√2 ) ist.