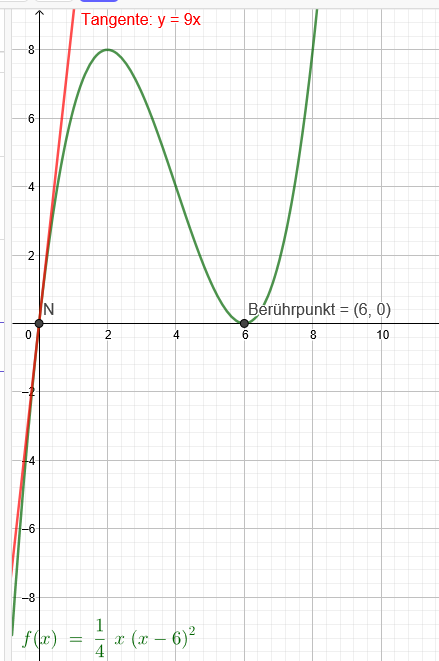
Eine ganzrationale Funktion 3. Grades verläuft durch den Koordinatenursprung, der Anstieg der Tangenten ist dort 9. Weiterhin berührt sie die \( x \) Achse bei \( x=6 \). Um welche Funktion handelt es sich?
Lösung über die Nullstellenform der kubischen Parabel:
\(f(x)=a*[x*(x-6)^2]\)
\(f´(x)=a*[1*(x-6)^2+x*2*(x-6)*1]\)
\(f´(0)=a*(0-6)^2=36a→36a=9→a=\frac{1}{4}\)
\(f(x)=\frac{1}{4}*x*(x-6)^2\)